题目内容
已知椭圆的短轴大于焦距,则它的离心率的取值范围是
(0,
)
| ||
| 2 |
(0,
)
.
| ||
| 2 |
分析:设出椭圆的标准方程,根据题意得2b>2c,即
>c,平方化简整理,即得该椭圆的离心率的取值范围.
| a2-c2 |
解答:解:设椭圆方程为
+
=1,其中a>b>0
∵椭圆的短轴大于焦距,
∴2b>2c,即
>c,整理得a2>2c2,
两边都除以a2,得1>2e2,即e2<
,得0<e<
∴椭圆离心率e的取值范围是:(0,
)
故答案为:(0,
)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的短轴大于焦距,
∴2b>2c,即
| a2-c2 |
两边都除以a2,得1>2e2,即e2<
| 1 |
| 2 |
| ||
| 2 |
∴椭圆离心率e的取值范围是:(0,
| ||
| 2 |
故答案为:(0,
| ||
| 2 |
点评:本题给出椭圆的短轴长大于焦距,求椭圆的离心率e的取值范围,着重考查了椭圆的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
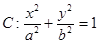 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点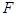 的最短距离为
的最短距离为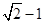 .
. 且斜率为
且斜率为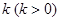 的直线
的直线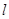 与
与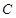 交于
交于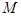 、
、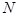 两点,
两点,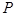 是点
是点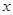 轴的对称点,证明:
轴的对称点,证明: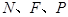 三点共线.
三点共线.