题目内容
设f(x)=3ax2+2bx+c若a+b+c=0,f(0)>0,f(1)>0,求证:(Ⅰ)a>0且-2<![]() <-1;
<-1;
(Ⅱ)方程f(x)=0在(0,1)内有两个实根.
证明:(Ⅰ)由f(0)>0,且f(1)>0得:
c>0且3a+2b+c>0.∵c=-a-b>0,
∴2a+b>0, (1)
-a-b>0. (2)
两式相加,得:a>0.
由(1)得![]() >-2,由(2)得
>-2,由(2)得![]() <-1,
<-1,
∴-2<![]() <-1.
<-1.
(Ⅱ)由于a>0,∴f(x)的图象是开口向上的抛物线.
又∵f(0)>0.f(1)>0抛物线的对称轴满足:0<![]() <-
<-![]() <
<![]() <1.
<1.
∴要证明f(x)=0在(0,1)内有两个实根,只需证明:
Δ=4b2-12ac>0,即可.
把c=-a-b 代入上式,即证:b2+3ab+3a2>0,
即证(b+![]() a)2+
a)2+![]() a2>0,
a2>0,
由于a>0,∴![]() a2>0,而(b+
a2>0,而(b+![]() a)2≥0,
a)2≥0,
∴(b+![]() a)2+
a)2+![]() a2>0成立.
a2>0成立.
从而方程f(x)=0在(0,1)内有两个实根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
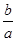 <-1
<-1