Question

【题目】疫情期间，某小区超市平面图如图所示，由矩形与扇形组成，米，米，，经营者决定在点处安装一个监控摄像头，摄像头的监控视角，摄像头监控区域为图中阴影部分，要求点在弧上，点在线段上.设.

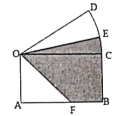
（1）求该监控摄像头所能监控到的区域面积关于的函数关系式，并求出的取值范围；

（2）求监控区域面积最大时，角的正切值.

Answer 1

【答案】（1），；

（2）

【解析】

（1）分别求得扇形和四边形的面积，加和得到，根据矩形长和宽可确定最小值，进而确定的范围；

（2）设，利用导数可求得的单调性，通过求得可求得，并确定所求的的正切值.

（1）扇形的面积为.

四边形的面积为,

阴影部分的面积为.

，其中，.

（2）设，则，

令，解得：，，

设其解为，即，则在上单调递减，在上单调递增，

，，此时

监控区域面积最大时，角的正切值为.