题目内容
(14分)已知函数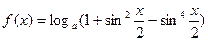 ,其中
,其中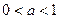 .
.
(1)判定函数 的奇偶性;
的奇偶性;
(2)函数 是否周期函数?若是,最小正周期是多少?
是否周期函数?若是,最小正周期是多少?
(3)试写出函数 的单调区间和最大值、最小值;
的单调区间和最大值、最小值;
(4)当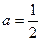 时,试研究关于
时,试研究关于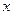 的方程
的方程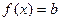 在
在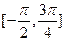 上的解的个数.
上的解的个数.
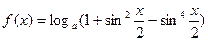 ,其中
,其中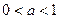 .
.(1)判定函数
 的奇偶性;
的奇偶性;(2)函数
 是否周期函数?若是,最小正周期是多少?
是否周期函数?若是,最小正周期是多少?(3)试写出函数
 的单调区间和最大值、最小值;
的单调区间和最大值、最小值;(4)当
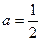 时,试研究关于
时,试研究关于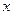 的方程
的方程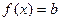 在
在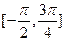 上的解的个数.
上的解的个数.(1)偶函数
(2)函数 是周期函数,最小正周期是
是周期函数,最小正周期是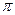
(3)函数 的单调递增区间为
的单调递增区间为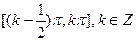 ;
;
函数 的单调递减区间为
的单调递减区间为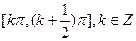
函数 的最大值为0;
的最大值为0;
函数 的最小值为
的最小值为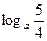
(4)方程有3个解
(2)函数
 是周期函数,最小正周期是
是周期函数,最小正周期是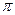
(3)函数
 的单调递增区间为
的单调递增区间为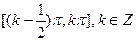 ;
;函数
 的单调递减区间为
的单调递减区间为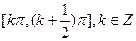
函数
 的最大值为0;
的最大值为0;函数
 的最小值为
的最小值为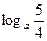
(4)方程有3个解
本题满分14分。第1小题3分,第2小题3分,第3小题4分,第1小题4分
(1)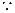 函数
函数 的定义域为R,关于原点对称, 1分
的定义域为R,关于原点对称, 1分
且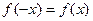 对
对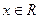 恒成立,
恒成立,
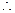 函数
函数 是偶函数。 2分
是偶函数。 2分
(2)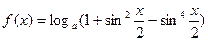
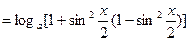
=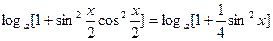
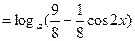 2分
2分
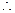 函数
函数 是周期函数,最小正周期是
是周期函数,最小正周期是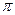 。 1分
。 1分
(3)函数 的单调递增区间为
的单调递增区间为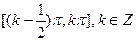 ;
;
(注:区间两端开或闭均可,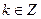 不扣分) 1分
不扣分) 1分
函数 的单调递减区间为
的单调递减区间为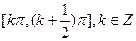
(注:区间两端开或闭均可,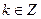 不扣分 ) 1分
不扣分 ) 1分
函数 的最大值为0; 1分
的最大值为0; 1分
函数 的最小值为
的最小值为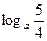 1分
1分
(4)由数形结合得,当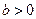 或
或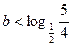 时,方程无解; 1分
时,方程无解; 1分
当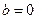 时方程有一个解; 1分
时方程有一个解; 1分
当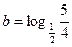 或
或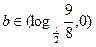 时方程有2个解; 1分
时方程有2个解; 1分
当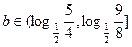 时方程有3个解. 1分
时方程有3个解. 1分
(注:以上区间的开闭错或讨论不全,均不给分)
(1)
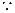 函数
函数 的定义域为R,关于原点对称, 1分
的定义域为R,关于原点对称, 1分且
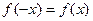 对
对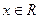 恒成立,
恒成立,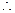 函数
函数 是偶函数。 2分
是偶函数。 2分(2)
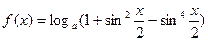
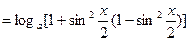
=
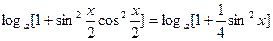
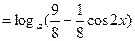 2分
2分 函数
函数 是周期函数,最小正周期是
是周期函数,最小正周期是 。 1分
。 1分(3)函数
 的单调递增区间为
的单调递增区间为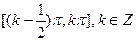 ;
;(注:区间两端开或闭均可,
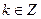 不扣分) 1分
不扣分) 1分函数
 的单调递减区间为
的单调递减区间为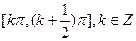
(注:区间两端开或闭均可,
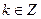 不扣分 ) 1分
不扣分 ) 1分函数
 的最大值为0; 1分
的最大值为0; 1分函数
 的最小值为
的最小值为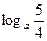 1分
1分(4)由数形结合得,当
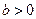 或
或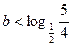 时,方程无解; 1分
时,方程无解; 1分当
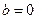 时方程有一个解; 1分
时方程有一个解; 1分当
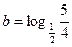 或
或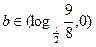 时方程有2个解; 1分
时方程有2个解; 1分当
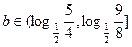 时方程有3个解. 1分
时方程有3个解. 1分(注:以上区间的开闭错或讨论不全,均不给分)

练习册系列答案
相关题目
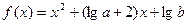 满足
满足 且对于任意
且对于任意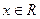 , 恒有
, 恒有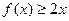 成立。
成立。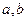 的值;
的值;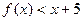 。
。 ,若对于任意的
,若对于任意的 ,都有
,都有 满足方程
满足方程 ,这时
,这时 的取值集合为
的取值集合为



 的定义域为_____ _____。
的定义域为_____ _____。 = .
= . 为常数),若
为常数),若 时,
时, 恒成立,则
恒成立,则 的取值范围是___________
的取值范围是___________  =lg(
=lg( -2)的定义域是 .
-2)的定义域是 . (
( 是自然对数的底数,
是自然对数的底数, )
) 的极大值;
的极大值; 是区间
是区间 上的任意两个实数,求证:
上的任意两个实数,求证: .
.