题目内容
直线y=kx+1与双曲线3x2-y2=1的左支交于点A，与右支交于点B．
（1）求实数k的取值范围；
（2）若以线段AB为直径的圆经过坐标原点，求k的取值．
（1）求实数k的取值范围；
（2）若以线段AB为直径的圆经过坐标原点，求k的取值．
考点：双曲线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：（1）由直线y=kx+1与双曲线3x2-y2=1，得（3-k2）x2-2kx-2=0，利用A，B在双曲线的左右两支上，根据韦达定理即可得不等式，解出即可；
（2）把存在实数k，使得以线段AB为直径的圆经过坐标原点转化为kOA•kOB=-1，即x1x2+y1y2=0，整理后代入根与系数关系求解实数k的值．
（2）把存在实数k，使得以线段AB为直径的圆经过坐标原点转化为kOA•kOB=-1，即x1x2+y1y2=0，整理后代入根与系数关系求解实数k的值．
解答：
解：（1）由直线y=kx+1与双曲线3x2-y2=1，得（3-k2）x2-2kx-2=0，
因为A．B在双曲线的左右两支上，所以3-k2≠0，
＜0，
解得-
＜k＜
；
（2）假设存在实数k，使得以线段AB为直径的圆经过坐标原点，设A（x1，y1），B（x2，y2），
则kOA•kOB=-1，即x1x2+y1y2=0，
∴x1x2+（kx1+1）（kx2+1）=0，
即（k2+1）x1x2+k（x1+x2）+1=0，
∴（k2+1）•
+k•
=0，
整理得k2=1，符合条件，
∴k=±1．
因为A．B在双曲线的左右两支上，所以3-k2≠0，
| -2 |
| 3-k2 |
解得-
| 3 |
| 3 |
（2）假设存在实数k，使得以线段AB为直径的圆经过坐标原点，设A（x1，y1），B（x2，y2），
则kOA•kOB=-1，即x1x2+y1y2=0，
∴x1x2+（kx1+1）（kx2+1）=0，
即（k2+1）x1x2+k（x1+x2）+1=0，
∴（k2+1）•
| -2 |
| 3-k2 |
| 2k |
| 3-k2 |
整理得k2=1，符合条件，
∴k=±1．
点评：本题主要考查了直线与双曲线的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系解题，是处理这类问题的最为常用的方法，训练了利用直线斜率的关系判断两直线的垂直关系，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
若不等式
≤μ≤
对任意的t∈（0，2]上恒成立，则μ的取值范围是（ ）
| t |
| t2+9 |
| ||
t+
|
A、[
| ||||||
B、[
| ||||||
C、[
| ||||||
D、[
|
设集合A={x|y=ln（x+1）}，B={-2，-1，0，1}，则（∁RA）∩B=（ ）
| A、{-2} |
| B、{-2，-1} |
| C、{-2，-1，0} |
| D、{-2，-1，0，1} |
对于推理：若a＞b，则a2＞b2，因为2＞-2，则22＞（-2）2，即4＞4，下列说法正确的是（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理正确 |
| D、不是演绎推理 |
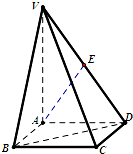如图，在四棱锥V-ABCD中，VA⊥底面ABCD，底面ABCD是边长为2的正方形．