��Ŀ����
(��)��֪����ͬ������F1��F2����Բ + y2=1(m>1)��˫���� - y2=1��n>0����P������
��һ�����㣬��F1PF2����״�� �� ��
A����������� B��ֱ�������� C������������ D����m��n�仯���仯
(��)��֪����ͬ������F1��F2����Բ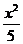 + y2=1��˫����
+ y2=1��˫����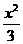 - y2=1��P�����ǵ�һ�����㣬
- y2=1��P�����ǵ�һ�����㣬
��F1PF2����״�� �� ��
A����������� B��ֱ�������� C������������ D������������
���𰸡�
B. ��ʾ����|PF1|+|PF2|=2��|PF1|-|PF2|=��2����m-1=n+1��
��|PF1|2+|PF2|2=2(m+n)=4(m-1)=|F1F2|2

��ϰ��ϵ�д�
 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
�����Ŀ
��֪����ͬ������F1��F2����Բ
+y2=1��˫����
-y2=1��P�����ǵ�һ�����㣬���F1PF2����״�ǣ�������
| x2 |
| 5 |
| x2 |
| 3 |
| A����������� |
| B��Bֱ�������� |
| C������������ |
| D������������ |
 + y2=1(m>1)��˫����
+ y2=1(m>1)��˫���� - y2=1��n>0����P�����ǵ�һ�����㣬��F1PF2����״�� �� ��
- y2=1��n>0����P�����ǵ�һ�����㣬��F1PF2����״�� �� ��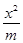 + y2=1(m>1)��˫����
+ y2=1(m>1)��˫����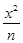 - y2=1��n>0����P�����ǵ�һ�����㣬��F1PF2����״�ǣ� ��
- y2=1��n>0����P�����ǵ�һ�����㣬��F1PF2����״�ǣ� ��