题目内容
已知有相同两焦点F1、F2的椭圆
+y2=1和双曲线
-y2=1，P是它们的一个交点，则△F1PF2的形状是（ ）
| x2 |
| 5 |
| x2 |
| 3 |
| A、锐角三角形 |
| B、B直角三角形 |
| C、钝有三角形 |
| D、等腰三角形 |
分析：由题设中的条件，设两个圆锥曲线的焦距为2c，椭圆的长轴长2
，双曲线的实轴长为2
，不妨令P在双曲线的右支上，根据椭圆和双曲线的性质以及勾股定理即可得到结论．
| 5 |
| 3 |
解答：解：由题意设两个圆锥曲线的焦距为2c，椭圆的长轴长2
，双曲线的实轴长为2
，不
妨令P在双曲线的右支上，由双曲线的定义|PF1|-|PF2|=2
①
由椭圆的定义|PF1|+|PF2|=2
②
①2+②2得|PF1|2+|PF2|2=4
又|F1F2|=4，
∴|PF1|2+|PF2|2=|F1F2|，
则△F1PF2的形状是直角三角形
故选B．
| 5 |
| 3 |
妨令P在双曲线的右支上，由双曲线的定义|PF1|-|PF2|=2
| 3 |
由椭圆的定义|PF1|+|PF2|=2
| 5 |
①2+②2得|PF1|2+|PF2|2=4
又|F1F2|=4，
∴|PF1|2+|PF2|2=|F1F2|，
则△F1PF2的形状是直角三角形
故选B．
点评：本题考查圆锥曲线的共同特征，考查通过椭圆与双曲线的定义求焦点三角形三边长，解决本题的关键是根据所得出的条件灵活变形，求出焦点三角形的边长来．
练习册系列答案
相关题目
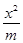+ y2=1(m>1)和双曲线
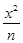- y2=1（n>0），P是它们的一个交点，则ΔF1PF2的形状是（ ）