题目内容
10.在平面直角坐标系xOy中,已知直线l:$\left\{\begin{array}{l}{x=2+t}\\{y=kt}\end{array}\right.$(t为参数)与圆C:$\left\{\begin{array}{l}{x=2+rcosθ}\\{y=rsinθ}\end{array}\right.$(θ为参数)相交于A,B两点,且|AB|=1.(1)求直线l与圆C的普通方程;
(2)求实数r的值.
分析 (1)消去参数,可得直线l与圆C的普通方程;
(2)由(1)知道,直线l过圆心,利用|AB|=1,即可求实数r的值.
解答 解:(1)直线l:$\left\{\begin{array}{l}{x=2+t}\\{y=kt}\end{array}\right.$(t为参数)的普通方程为y=k(x-2),过点(2,0)
圆C:$\left\{\begin{array}{l}{x=2+rcosθ}\\{y=rsinθ}\end{array}\right.$(θ为参数)的普通方程为(x-2)2+y2=r2,圆心为(2,0)
(2)由(1)知道,直线l过圆心,
∵|AB|=1,
∴r=$\frac{1}{2}$.
点评 本题考查参数方程化为普通方程,考查直线与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
15.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点恰为抛物线y2=2px的焦点F,设抛物线的准线l与x轴的交点为M,过F的直线与抛物线交于A,B两点,若以|BM|为直径的圆过点A,则|AB|=( )
| A. | 2$\sqrt{5}$-2 | B. | 4 | C. | 2$\sqrt{5}$+2 | D. | 4$\sqrt{5}$ |
 在△ABC中,a、b、c分别为内角A、B、C的对边.若a=1,c=$\sqrt{2}$,cosC=$\frac{3}{4}$.
在△ABC中,a、b、c分别为内角A、B、C的对边.若a=1,c=$\sqrt{2}$,cosC=$\frac{3}{4}$.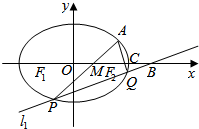 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.