题目内容
已知a∈R,若关于x的方程x2+x+|a- |+|a|=0有实根,求a的取值.
|+|a|=0有实根,求a的取值.
解:由x2+x+|a- |+|a|=0得-x2-x=|a-
|+|a|=0得-x2-x=|a- |+|a|,
|+|a|,
设f(x)=-x2-x,则 ,
,
所以要使关于x的方程x2+x+|a- |+|a|=0有实根,
|+|a|=0有实根,
则|a- |+|a|
|+|a|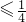 ,
,
因为|a- |+|a|
|+|a|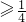 ,所以|a-
,所以|a- |+|a|=
|+|a|= ,
,
此时0 .
.
分析:将方程x2+x+|a- |+|a|=0转化为-x2-x=|a-
|+|a|=0转化为-x2-x=|a- |+|a|,设f(x)=-x2-x,利用二次函数的性质确定a的取值范围.
|+|a|,设f(x)=-x2-x,利用二次函数的性质确定a的取值范围.
点评:本题主要考查二次函数的性质以及绝对值的几何意义.
 |+|a|=0得-x2-x=|a-
|+|a|=0得-x2-x=|a- |+|a|,
|+|a|,设f(x)=-x2-x,则
 ,
,所以要使关于x的方程x2+x+|a-
 |+|a|=0有实根,
|+|a|=0有实根,则|a-
 |+|a|
|+|a|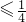 ,
,因为|a-
 |+|a|
|+|a|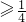 ,所以|a-
,所以|a- |+|a|=
|+|a|= ,
,此时0
 .
.分析:将方程x2+x+|a-
 |+|a|=0转化为-x2-x=|a-
|+|a|=0转化为-x2-x=|a- |+|a|,设f(x)=-x2-x,利用二次函数的性质确定a的取值范围.
|+|a|,设f(x)=-x2-x,利用二次函数的性质确定a的取值范围.点评:本题主要考查二次函数的性质以及绝对值的几何意义.

练习册系列答案
相关题目
 选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)
选做题(考生只能从A,B,C中选做一题,多做以所做第一题记分)