题目内容
设f(x)=
(1)将函数 的图象向左平移
的图象向左平移 个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图象,求
的图象,求 .并用“五点法”画出y=g(x), x∈[0,π]的图像。
.并用“五点法”画出y=g(x), x∈[0,π]的图像。
(2)若关于x的方程g(x)= k+1在 内有两个不同根α、β,求α+β的值及k的取值范围.
内有两个不同根α、β,求α+β的值及k的取值范围.
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
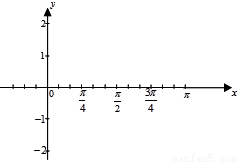
【答案】
①y=2sin(2x+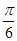 )
)
②可在同一坐标系中画出函数y=sin(2x+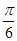 )及y=
)及y= 的图象,借助于图象的直观性求解.设C:y=y=sin(2x+
的图象,借助于图象的直观性求解.设C:y=y=sin(2x+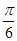 ),l:y=
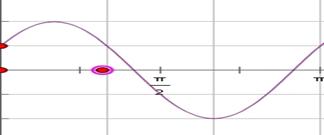
),l:y= ,在同一坐标系中作出它们的图象如下图.
,在同一坐标系中作出它们的图象如下图.

由图易见当 ≤
≤ <1时,即0≤k<1时,直线l与曲线C有两个交点,且两交点的横坐标为α、β,从图象中还可看出α、β关于x=
<1时,即0≤k<1时,直线l与曲线C有两个交点,且两交点的横坐标为α、β,从图象中还可看出α、β关于x= 对称,故α+β=
对称,故α+β= .综上可知,0≤k<1,且α+β=
.综上可知,0≤k<1,且α+β= .
.
【解析】略

练习册系列答案
相关题目
设f(x)=
,g(x)=ax+5-2a(a>0),若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,则实数a的取值范围是( )
| 2x2 |
| x+1 |
A、[
| ||||
B、[-
| ||||
| C、[1,4] | ||||
D、[
|