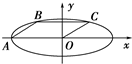
题目内容
如图所示,已知椭圆ax2+by2=1与直线x+y-1=0交于A、B两点,|AB|=2
思路解析:由已知弦长,可联立方程组根据韦达定理建立关系式求解.
解:设A(x1,y1)、B(x2,y2),线段AB的中点为M(x0,y0).
由 得(a+b)x2-2bx+b-1=0.
得(a+b)x2-2bx+b-1=0.
由根与系数的关系,得
∴x0=![]() =
=![]() .
.
又∵M(x0,y0)在直线x+y-1=0上,∴y0=1-x0=![]() .
.
故OM的斜率为![]() =
=![]() =
=![]() ①.
①.
又|AB|=![]() |x1-x2|=
|x1-x2|=![]()
![]()
=![]()
![]() =
= =2
=2![]() ②.
②.
由①②知
深化升华
直线l与椭圆![]() +
+![]() =1(a>b>0)交于A、B两点,线段AB的中点为M,则l的斜率kl与OM(O为坐标原点)的斜率kOM的积kl·kOM=-
=1(a>b>0)交于A、B两点,线段AB的中点为M,则l的斜率kl与OM(O为坐标原点)的斜率kOM的积kl·kOM=-![]() (两直线斜率均存在时),本题若用这一结论求解会更简单.
(两直线斜率均存在时),本题若用这一结论求解会更简单.

练习册系列答案
相关题目
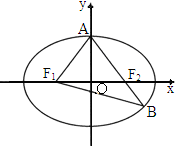
 如图所示,已知椭圆的方程为
如图所示,已知椭圆的方程为 (文)如图所示:已知椭圆C:
(文)如图所示:已知椭圆C: 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 如图所示,已知椭圆C:
如图所示,已知椭圆C: (a>b>0),
(a>b>0), 、
、 分别为椭圆的左、右焦点,A为椭圆的上顶点,直线
分别为椭圆的左、右焦点,A为椭圆的上顶点,直线 交椭圆于另一点B.
交椭圆于另一点B.
 ,求椭圆的离心率;
,求椭圆的离心率;
 ,求椭圆的方程.
,求椭圆的方程.