题目内容
一个不透明的袋中装有白球、红球共9个(9个球除颜色外其余完全相同),经充分混合后,从袋中随机摸出2球,且摸出的2球中至少有一个是白球的概率为| 5 | 6 |
分析:由题意设白球个数为x,则红球个数为9-x,利用从袋中随机摸出2球,且摸出的2球中至少有一个是白球的概率为
,解出x的值,由题意ξ表示摸出的2个球中红球的个数,可以取0,1,2.利用离散型随即变量的定义及分布列定义和期望定义即可求解.
| 5 |
| 6 |
解答:解:由于从袋中随机摸出2球,且摸出的2球中至少有一个是白球的概率为
,设白球个数为x,则红球个数为9-x,
则可以得到:
=
?x=5或x=-20(舍),所以白球个数为5,红球个数为4,
由于ξ表示摸出的2个球中红球的个数,由题意ξ表示摸出的2个球中红球的个数ξ=0,1,2,
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,
所以该随机变量的分布列为:
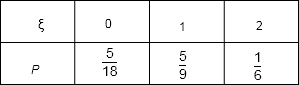
利用期望的定义得:Eξ=0×
+1×
+2×
=
.
故答案为:
.
| 5 |
| 6 |
则可以得到:
| ||||||
|
| 5 |
| 6 |
由于ξ表示摸出的2个球中红球的个数,由题意ξ表示摸出的2个球中红球的个数ξ=0,1,2,
P(ξ=0)=
| ||
|
| 5 |
| 18 |
| ||||
|
| 5 |
| 9 |
| ||
|
| 1 |
| 6 |
所以该随机变量的分布列为:

利用期望的定义得:Eξ=0×
| 5 |
| 18 |
| 5 |
| 9 |
| 1 |
| 6 |
| 8 |
| 9 |
故答案为:
| 8 |
| 9 |
点评:此题考查了方程的思想,组合数记数原理及离散型随机变量的定义及分布列,还考查了离散型随即变量的期望.

练习册系列答案
相关题目