题目内容
设平面向量 =(cosx,sinx),
=(cosx,sinx),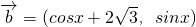 ,
,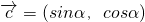 ,x∈R,
,x∈R,
(Ⅰ)若 ,求cos(2x+2α)的值;
,求cos(2x+2α)的值;
(Ⅱ)若 ,证明
,证明 和
和 不可能平行;
不可能平行;
(Ⅲ)若α=0,求函数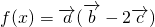 的最大值,并求出相应的x值.
的最大值,并求出相应的x值.
解:(Ⅰ)若 ,则
,则  ,cosxsinα+sinxcosα=0,sin(x+α)=0
,cosxsinα+sinxcosα=0,sin(x+α)=0
所以,cos(2x+2α)=1-2sin2(x+α)=1.
(Ⅱ)假设 与
与 平行,则
平行,则 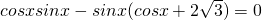 ,即 sinx=0,
,即 sinx=0,
而 时,sinx>0,矛盾,故
时,sinx>0,矛盾,故  和
和 不可能平行.
不可能平行.
(Ⅲ)若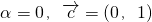 ,
,
则
=cosx =1-2sinx+2
=1-2sinx+2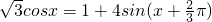 ,
,
所以,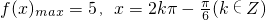 .
.
分析:(Ⅰ)利用两个向量垂直,它们的数量积等于0,以及二倍角的余弦公式求得cos(2x+2α)的值.
(Ⅱ)假设 与
与 平行,则
平行,则 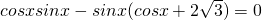 ,即 sinx=0,与已知矛盾.
,即 sinx=0,与已知矛盾.
(Ⅲ)若α=0,则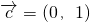 ,函数
,函数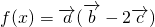 ═1-2sinx+2
═1-2sinx+2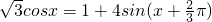 ,
,
利用正弦函数的有界性求出函数的最值.
点评:本题考查两个向量的数量积公式的应用,两个向量平行、垂直的性质,两个向量坐标形式的运算.
 ,则
,则  ,cosxsinα+sinxcosα=0,sin(x+α)=0
,cosxsinα+sinxcosα=0,sin(x+α)=0所以,cos(2x+2α)=1-2sin2(x+α)=1.
(Ⅱ)假设
 与
与 平行,则
平行,则 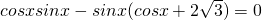 ,即 sinx=0,
,即 sinx=0,而
 时,sinx>0,矛盾,故
时,sinx>0,矛盾,故  和
和 不可能平行.
不可能平行.(Ⅲ)若
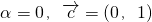 ,
,则

=cosx
 =1-2sinx+2
=1-2sinx+2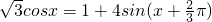 ,
,所以,
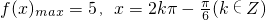 .
.分析:(Ⅰ)利用两个向量垂直,它们的数量积等于0,以及二倍角的余弦公式求得cos(2x+2α)的值.
(Ⅱ)假设
 与
与 平行,则
平行,则 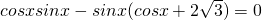 ,即 sinx=0,与已知矛盾.
,即 sinx=0,与已知矛盾.(Ⅲ)若α=0,则
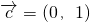 ,函数
,函数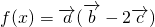 ═1-2sinx+2
═1-2sinx+2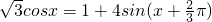 ,
,利用正弦函数的有界性求出函数的最值.
点评:本题考查两个向量的数量积公式的应用,两个向量平行、垂直的性质,两个向量坐标形式的运算.

练习册系列答案
相关题目
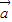 =(a1,a2),
=(a1,a2),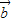 =(b1,b2),且
=(b1,b2),且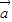 与
与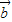 的夹角为θ,
的夹角为θ,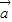 •
•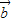 =|
=|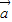 ||
||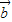 |cosθ,
|cosθ,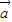 •
•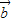 ≤|
≤|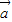 ||
||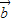 |.
|.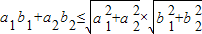 ,
,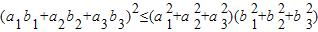 成立;
成立;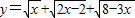 的最大值.
的最大值.