题目内容
设平面向量
=(cosα，sinα)，
=(-
，
)．
①求证：向量
+
与
-
垂直．
②当两个向量
+
与
-
的模相等时，且α∈(0，
)，求角α．
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
①求证：向量
| a |
| b |
| a |
| b |
②当两个向量
| 3 |
| a |
| b |
| a |
| 3 |
| b |
| π |
| 2 |
分析：①根据两个向量的坐标求出它们的模，计算 (
+
)•(
-
)=0，可得向量
+
与
-
垂直．
②求出
+
的坐标，可得它的模，再求出
-
的坐标，可得它的模．根据两个向量的模相等可得tanα=
，由此求得α 的值．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②求出
| 3 |
| a |
| b |
| a |
| 3 |
| b |
| ||
| 3 |
解答：解：①证明：∵
=(cosα，sinα)，
=(-
，
)，
∴|
|=1，|
|=1，(
+
)•(
-
)=
2-
2=0，
向量
+
与
-
垂直．
②∵
+
=（
cosα-
，
sinα+
），
|
+
|=
=-
cosα+3sinα+4．
-
=（cosα+
，sinα-
），
|
-
|=
=
cosα-3sinα+4．
由两个向量
+
与
-
的模相等可得-
cosα+3sinα+4=
cosα-3sinα+4，
解得tanα=
，又α∈(0，
)，
∴α=
．
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
∴|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
向量
| a |
| b |
| a |
| b |
②∵
| 3 |
| a |
| b |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
|
| 3 |
| a |
| b |
(3cosα -
|
| 3 |
| a |
| 3 |
| b |
| ||
| 2 |
| 3 |
| 2 |
|
| a |
| 3 |
| b |
(cosα+
|
| 3 |
由两个向量
| 3 |
| a |
| b |
| a |
| 3 |
| b |
| 3 |
| 3 |
解得tanα=
| ||
| 3 |
| π |
| 2 |
∴α=
| π |
| 6 |
点评：本题主要考查两个向量垂直的性质，两个向量坐标形式的运算，求向量的模的方法，属于中档题．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
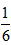），且a∥b，求sin2α的值。