Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥ ≥∆∑≥ßő™Ńňľž≤ťľ◊°Ę““ŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń…ķ≤ķ«ťŅŲ£¨ňśĽķ‘ŕ’‚ŃĹŐűŃųňģŌŖ…Ōłų≥ť»°40ľĢ≤ķ∆∑◊ųő™—ýĪĺ£¨≤Ę≥∆≥ŲňŁ√«Ķń÷ōŃŅ£®Ķ•őĽ£ļŅň£©£¨÷ōŃŅ÷Ķ¬š‘ŕ![]() ńŕĶń≤ķ∆∑ő™ļŌłŮ∆∑£¨∑Ů‘Úő™≤ĽļŌłŮ∆∑.
ńŕĶń≤ķ∆∑ő™ļŌłŮ∆∑£¨∑Ů‘Úő™≤ĽļŌłŮ∆∑.
◊Ę£ļĪŪ1 «ľ◊ŃųňģŌŖ—ýĪĺĶń∆Ķ ż∑÷≤ľĪŪ£¨Õľ1 «““ŃųňģŌŖ—ýĪĺĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ.
≤ķ∆∑÷ōŃŅ£®Ņň£© | ∆Ķ ż |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
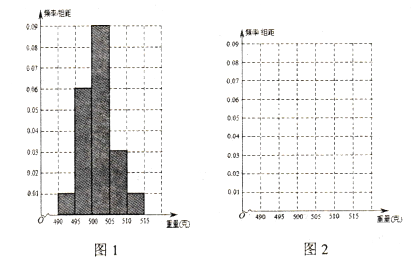
£®1£©łýĺ›…Ō√śĪŪ1÷–Ķń żĺ›‘ŕÕľ2÷–◊ų≥Ųľ◊ŃųňģŌŖ—ýĪĺĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£Ľ
£®2£©»Ű“‘∆Ķ¬ ◊ųő™łŇ¬ £¨ ‘Ļņľ∆ī”ŃĹŐűŃųňģŌŖ…Ō∑÷Īū»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ∑÷Īū «∂ŗ…Ŕ£Ľ
£®3£©”…“‘…ŌÕ≥ľ∆ żĺ›ÕÍ≥…Ō¬√ś![]() Ń–Ń™ĪŪ£¨≤ĘĽōīū”–∂ŗīůĶńį—ő’»Ōő™≤ķ∆∑ĶńįŁ◊į÷ ŃŅ”ŽŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń—°‘Ů”–Ļō.
Ń–Ń™ĪŪ£¨≤ĘĽōīū”–∂ŗīůĶńį—ő’»Ōő™≤ķ∆∑ĶńįŁ◊į÷ ŃŅ”ŽŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń—°‘Ů”–Ļō.
ľ◊ŃųňģŌŖ | ““ŃųňģŌŖ | ļŌľ∆ | |
ļŌłŮ | |||
≤ĽļŌłŮ | |||
ļŌľ∆ |
≤őŅľĻę Ĺ£ļ![]() £¨∆š÷–
£¨∆š÷–![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£Ľ£®2£©ī”ľ◊ŃųňģŌŖ…Ō»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ő™![]() £Ľī”““ŃųňģŌŖ…Ō»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ő™0.9.£®3£©ľŻĹ‚őŲ
£Ľī”““ŃųňģŌŖ…Ō»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ő™0.9.£®3£©ľŻĹ‚őŲ
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›ňýłÝĶń√Ņ“Ľ◊ťĶń∆Ķ żļÕ—ýĪĺ»›ŃŅ«ů≥Ų√Ņ“Ľ◊ťĶń∆Ķ¬ £¨◊ų≥Ų∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ£ģ
£®2£©łýĺ›ňýłÝĶń—ýĪĺ÷–ĶńļŌłŮ∆∑ ż£¨≥ż“‘—ýĪĺ»›ŃŅ◊Ų≥ŲļŌłŮ∆∑Ķń∆Ķ¬ £¨Ņ…Ļņľ∆ī”ŃĹŐűŃųňģŌŖ…Ō»ő»°“ĽľĢ≤ķ∆∑ł√≤ķ∆∑ő™ļŌłŮ∆∑ĶńłŇ¬ £Ľ
£®3£©łýĺ›ňýłÝĶń żĺ›£¨Ń–≥ŲŃ–Ń™ĪŪ£¨łýĺ›ňýłÝĶńĻŘ≤‚÷ĶĶńĻę Ĺ£¨īķ»Ž żĺ›«ů≥ŲĻŘ≤‚÷Ķ£¨Õ¨ŃŔĹÁ÷ĶĹÝ––Ī»ĹŌ£¨Ķ√ĶĹ”–90%Ķńį—ő’»Ōő™≤ķ∆∑ĶńįŁ◊į÷ ŃŅ”ŽŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń—°‘Ů”–Ļō£ģ
£®1£©ľ◊ŃųňģŌŖ—ýĪĺĶń∆Ķ¬ ∑÷≤ľ÷Ī∑ĹÕľ»ÁŌ¬£ļ

£®2£©”…ĪŪ1÷™ľ◊ŃųňģŌŖ—ýĪĺ÷–ļŌłŮ∆∑ żő™![]() £¨
£¨
Ļ ľ◊ŃųňģŌŖ—ýĪĺ÷–ļŌłŮ∆∑Ķń∆Ķ¬ ő™![]() £¨
£¨
”…Õľ1÷™““ŃųňģŌŖ—ýĪĺ÷–ļŌłŮ∆∑Ķń∆Ķ¬ ő™![]() £¨
£¨
ĺ›īňŅ…Ļņľ∆ī”ľ◊ŃųňģŌŖ…Ō»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ő™![]() £Ľ
£Ľ
ī”““ŃųňģŌŖ…Ō»ő»°1ľĢ≤ķ∆∑£¨ł√≤ķ∆∑«°ļ√ «ļŌłŮ∆∑ĶńłŇ¬ ő™0.9.
£®3£©”…£®2£©÷™ľ◊ŃųňģŌŖ—ýĪĺ÷–ļŌłŮ∆∑ żő™30£¨““ŃųňģŌŖ—ýĪĺ÷–ļŌłŮ∆∑ żő™![]() .
.
![]() Ń–Ń™ĪŪ»ÁŌ¬£ļ
Ń–Ń™ĪŪ»ÁŌ¬£ļ
ľ◊ŃųňģŌŖ | ““ŃųňģŌŖ | ļŌľ∆ | |
ļŌłŮ | 30 | 36 | 66 |
≤ĽļŌłŮ | 10 | 4 | 14 |
ļŌľ∆ | 40 | 40 | 80 |
°Ŗ![]() £¨
£¨
°ŗ”–![]() Ķńį—ő’»Ōő™≤ķ∆∑ĶńįŁ◊į÷ ŃŅ”ŽŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń—°‘Ů”–Ļō.
Ķńį—ő’»Ōő™≤ķ∆∑ĶńįŁ◊į÷ ŃŅ”ŽŃĹŐű◊‘∂ĮįŁ◊įŃųňģŌŖĶń—°‘Ů”–Ļō.

 √Ņ»’10∑÷÷”Ņŕň„–ńň„ňŔň„ŐžŐžŃ∑ŌĶŃ–īūįł
√Ņ»’10∑÷÷”Ņŕň„–ńň„ňŔň„ŐžŐžŃ∑ŌĶŃ–īūįł