Question

【题目】已知椭圆C： （a＞b＞0）过点（1， ），离心率为 ，过椭圆右顶点A的两条斜率乘积为﹣ 的直线分别交椭圆C于M，N两点．
（1）求椭圆C的标准方程；
（2）直线MN是否过定点D？若过定点D，求出点D的坐标；若不过，请说明理由．

Answer 1

【答案】
（1）解：由已知 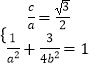，∴a=2，b=1，

∴椭圆C的标准方程为 ；

（2）解：直线MN过定点D（0，0）．

证明如下：由题意，A（2，0），直线AM和直线AN的斜率存在且不为0，

设AM的方程为y=k（x﹣2），代入椭圆方程得（1+4k2）x2﹣16k2x+16k2﹣4=0

∴2xM= ，

∴xM= ，

∴yM=k（xM﹣2）= ，

∴M（ ， ），

∵椭圆右顶点A的两条斜率乘积为﹣ 的直线分别交椭圆C于M，N两点，

∴设直线AN的方程为y=﹣ （x﹣2），

同理可得N（ ， ），

xM≠xN，即k 时，kMN= ，

∴直线MN的方程为y﹣ = （x﹣ ），即y= x，

∴直线MN过定点D（0，0）．

xM=xN，即k= 时，直线MN过定点D（0，0）．

综上所述，直线MN过定点D（0，0）

【解析】（1）由椭圆C： （a＞b＞0）过点（1， ），离心率为 ，建立方程，求出a，b，即可求椭圆C的标准方程；（2）设AM、AN的方程，代入椭圆方程，求出M，N的坐标，进而可得MN的方程，即可得出结论．