题目内容
已知数列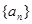 满足
满足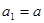 ,
,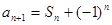 ,
,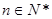 ,且
,且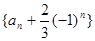 是等比数列。
是等比数列。
(Ⅰ)求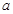 的值;
的值;
(Ⅱ)求出通项公式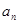 ;
;
(Ⅲ)求证: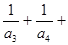 …
…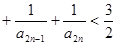
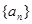 满足
满足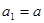 ,
,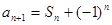 ,
,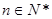 ,且
,且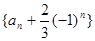 是等比数列。
是等比数列。(Ⅰ)求
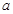 的值;
的值;(Ⅱ)求出通项公式
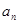 ;
;(Ⅲ)求证:
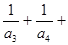 …
…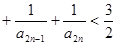
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.试题分析:(Ⅰ)
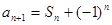 ,这是已知
,这是已知 型求
型求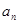 ,可利用
,可利用 ,来求出递推式,得
,来求出递推式,得 ,由
,由 得数列
得数列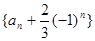 得公比为
得公比为 ,由
,由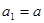 ,求出
,求出 ,则
,则 ,从而可求出
,从而可求出 ;(Ⅱ)求出通项公式
;(Ⅱ)求出通项公式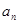 ,由(Ⅰ)知数列
,由(Ⅰ)知数列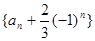 是以
是以 为首项,2为公比的等比数列,这样能写出
为首项,2为公比的等比数列,这样能写出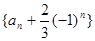 的通项公式,从而可得数列
的通项公式,从而可得数列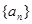 的通项公式
的通项公式 ;(Ⅲ)求证:
;(Ⅲ)求证: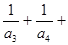 …
…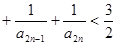 ,观察式子,当
,观察式子,当 时,
时,
 ,这样相邻两项相加,相邻两项相加,得到一个等比数列,利用等比数列的前n项和公式,即可证得.
,这样相邻两项相加,相邻两项相加,得到一个等比数列,利用等比数列的前n项和公式,即可证得.试题解析:(1)当
 时,
时,



又
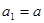
 又
又

 5分
5分(Ⅱ)由(1)知
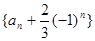 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列 ,
, 7分
7分(Ⅲ)当
 时,
时,
 10分
10分将
 由2到
由2到 赋值并累加得:
赋值并累加得: …
… …
…
 13分
13分
练习册系列答案
相关题目
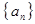 中,
中,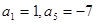 ,
,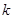 项和
项和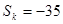 ,求
,求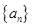 为等差数列,且
为等差数列,且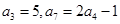 .
.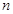 项和
项和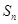 ;
;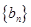 满足
满足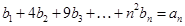 求数列
求数列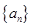 满足
满足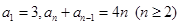
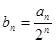 ,求数列
,求数列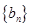 的前
的前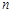 项和
项和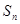 .
.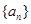 为等差数列,数列
为等差数列,数列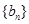 为等比数列,若
为等比数列,若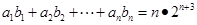 ,且
,且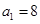 .
.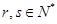 ,使得
,使得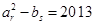 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的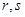 ;若不存在,请说明理由.
;若不存在,请说明理由.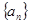 ,则
,则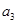 的所有取值中的最小值是( )
的所有取值中的最小值是( ) 中
中 ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 为
为 的最大值
的最大值

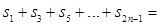 .
.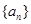 中,若
中,若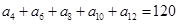 ,则
,则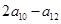 的值为 ( )
的值为 ( )