题目内容
4.在1,2,3,4,5,6这6个自然数中,任取3个不同的数.(1)求这3个数中至少有1个是偶数的概率;
(2)设ξ为这3个数中最大数与最小数的差(例如:若取出的数为1,2,4,此时ξ等于3).求随机变量ξ的分布列及其数学期望Eξ.
分析 (1)本题是一个等可能事件的概率,试验发生包含的事件是满足条件的事件是至少有一个是偶数,20-1=19种结果,得到概率.
(2)写出随机变量的所有取值,利用古典概型的概率公式求出随机变量取每一个值的概率值,列出分布列,利用随机变量的期望公式求出数学期望Eξ.
解答 解:(1)由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是从6个数字中任取3个,共有C63=20种结果,
满足条件的事件是至少有一个是偶数,20-1=19种结果,
记“这3个数至少有一个是偶数”为事件A,
∴P(A)=$\frac{19}{20}$,
即3个数中至少有1个是偶数的概率是$\frac{19}{20}$.
(2)ξ的取值为2,3,4,5,则
ξ=2时,所取数为123,234,345,456,概率为$\frac{1}{5}$;ξ=3时,所取数为124,134,235,245,346,356,概率为$\frac{3}{10}$;
ξ=4时,所取数为125,135,145,236,246,256,概率为$\frac{1}{5}$;ξ=5时,所取数为126,136,146,156,概率为$\frac{3}{10}$
所以随机变量ξ的分布列为
| ξ | 2 | 3 | 4 | 5 |
| P | $\frac{1}{5}$ | $\frac{3}{10}$ | $\frac{1}{5}$ | $\frac{3}{10}$ |
点评 利用古典概型求事件的概率要求出事件包含的基本事件的个数,常用的求法有:列举法、列表法、排列组合的方法、树状图法;求随机变量的分布列应该求出随机变量取每一个值的概率值.

练习册系列答案
相关题目
14.从区间[0,$\frac{π}{2}$]内随机取一个实数x,则sinx<$\frac{\sqrt{3}}{2}$的概率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
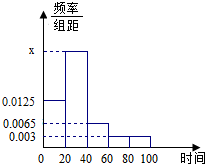 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].