题目内容
下面四个条件:① +
+ =
= 且
且 -
- =
= ;②
;② +x2
+x2 =0(x1,x2∈R);③
=0(x1,x2∈R);③ =λ
=λ 且λ唯一(λ∈R且
且λ唯一(λ∈R且 ≠0);④
≠0);④ +
+ =0(x,y∈R且x+y=0)其中能使
=0(x,y∈R且x+y=0)其中能使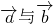 共线的是
共线的是
- A.①②
- B.①③
- C.②④
- D.③④
B
分析:向量共线的充要条件: 判断出①③;利用
判断出①③;利用 ?
? 判断出③④
判断出③④
解答:对于① 得
得 ,故
,故 ,故共线
,故共线
对于②,当x1=x2=0时,满足条件的向量是任意的,得不到
对于③两向量共线的充要条件是 ,能得到
,能得到
对于④, ?
? 故④推不出
故④推不出
故选B
点评:本题考查向量共线的充要条件,利用充要条件判断向量是否共线.
分析:向量共线的充要条件:
 判断出①③;利用
判断出①③;利用 ?
? 判断出③④
判断出③④解答:对于①
 得
得 ,故
,故 ,故共线
,故共线对于②,当x1=x2=0时,满足条件的向量是任意的,得不到

对于③两向量共线的充要条件是
 ,能得到
,能得到
对于④,
 ?
? 故④推不出
故④推不出故选B
点评:本题考查向量共线的充要条件,利用充要条件判断向量是否共线.

练习册系列答案
相关题目