题目内容
对于任意的实数x，不等式|x+1|≥kx恒成立，则实数k的取值范围是
- A.（-∞，0）
- B.[-1，0]
- C.[0，1]
- D.[0，∞）
C
分析：由题意得 y=|x+1|的图象不能在 y=kx 的图象的下方，如图所示：可得 0≤k≤1．
解答：
解：∵不等式|x+1|≥kx恒成立，
∴y=|x+1|的图象不能在 y=kx 的图象的下方，如图所示：
∴0≤k≤1，故选 C．
点评：本题考查函数的恒成立问题，体现了数形结合的数学思想．
分析：由题意得 y=|x+1|的图象不能在 y=kx 的图象的下方，如图所示：可得 0≤k≤1．
解答：
解：∵不等式|x+1|≥kx恒成立，∴y=|x+1|的图象不能在 y=kx 的图象的下方，如图所示：
∴0≤k≤1，故选 C．
点评：本题考查函数的恒成立问题，体现了数形结合的数学思想．
练习册系列答案
相关题目
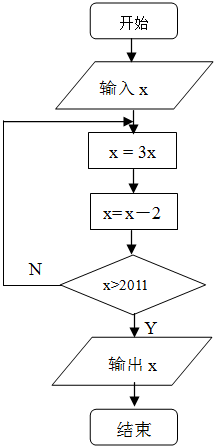如图所示程序框图表示：输入的实数x经过循环结构的一系列运算后，输出满足条件“x＞2011？”的第一个结果．但是程序不是对于任意的实数x都适用，为了保证程序能够顺利输出x，那么输入实数x时需要提示（ ）