题目内容
设函数f(x)=xm+ax的导数f′(x)=2x+3,则数列{
}(n∈N*)的前n项和是( )
| 1 |
| f(n)+2 |
A.
| B.
| C.
| D.
|
∵f(x)=xm+ax的导数f'(x)=mxm-1+a=2x+3,
∴m=2,a=3,
∴f(x)=x2+3x,
设an=
,
∴则an=
=
=
=
-
,
∴数列{
}(n∈N*)的前n项和
Sn=a1+a2+…+an
=(
-
)+(
-
)+…+(
-
)
=
-
=
.
故选B.
∴m=2,a=3,
∴f(x)=x2+3x,
设an=
| 1 |
| f(n)+2 |
∴则an=
| 1 |
| f(n)+2 |
| 1 |
| n2+3n+2 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴数列{
| 1 |
| f(n)+2 |
Sn=a1+a2+…+an
=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| n+2 |
=
| n |
| 2(n+2) |
故选B.

练习册系列答案
相关题目
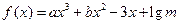 ,在
,在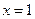 和
和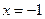 时取得极值,若对任意
时取得极值,若对任意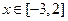 都有
都有 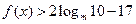 恒成立,求实数
恒成立,求实数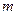 的取值集合.
的取值集合.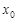 是函数
是函数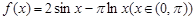 的零点,
的零点,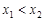 ,则:①
,则:①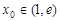 ;②
;②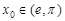 ;
;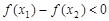 ;④
;④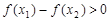 ,其中正确的命题是( )
,其中正确的命题是( )