题目内容
(2011•甘肃一模)设{an},{bn}都是各项为正数的数列,对任意的正整数n,都有an,bn2,an+1成等差数列,bn2,an+1,bn+12成等比数列.
(1)证明数列{bn}是等差数列;
(2)如果a1=2,b1=2,记数列{
}的前n项和为Sn,求证:Sn<1(n∈N*.)
(1)证明数列{bn}是等差数列;
(2)如果a1=2,b1=2,记数列{
| 1 | an |
分析:由题意可得,2bn2=an+an+1①an+12=bn2bn+12②
(1)结合已知条件an>0,bn>0及②得an+1=bnbn+1从而当n≥2时,an=bn-1bn结合①,2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1(n≥2)从而可得数列{bn}是等差数列
(2)由a1=2,b1=2及①得a2=6,再由②得b2=3从而有a2=6,b2=3从而可得等差数列{bn}的首项b1=2公差 d=b2-b1=1 通项公式bn=2+(n-1)=n+1又 an=bn-1bn=n(n+1可得数列{an}通项公式为an=n(n+1)
则
=
=
-
,利用裂项求和可求Sn,可证
(1)结合已知条件an>0,bn>0及②得an+1=bnbn+1从而当n≥2时,an=bn-1bn结合①,2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1(n≥2)从而可得数列{bn}是等差数列
(2)由a1=2,b1=2及①得a2=6,再由②得b2=3从而有a2=6,b2=3从而可得等差数列{bn}的首项b1=2公差 d=b2-b1=1 通项公式bn=2+(n-1)=n+1又 an=bn-1bn=n(n+1可得数列{an}通项公式为an=n(n+1)
则
| 1 |
| an |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:由题意可得,2bn2=an+an+1①an+12=bn2bn+12②
(1)∵an>0,bn>0
∴由②得an+1=bnbn+1
从而当n≥2时,an=bn-1bn
代入①,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1(n≥2)
∴数列{bn}是等差数列
(2)∵a1=2,b1=2
∴由①得a2=6,再由②得b2=3
等差数列{bn}的首项b1=2公差 d=b2-b1=1∴bn=2+(n-1)=n+1
当n≥2时,an=bn-1bn=n(n+1),当n=1时,a1=2也成立
∴数列{an}通项公式为an=n(n+1)
∴
=
=
-
数列{
}的前n项和Sn=
+
+…+
=1-
+
-
+…+
-
=1-
=
∴Sn<1
(1)∵an>0,bn>0
∴由②得an+1=bnbn+1
从而当n≥2时,an=bn-1bn
代入①,得2bn2=bn-1bn+bnbn+1
即2bn=bn-1+bn+1(n≥2)
∴数列{bn}是等差数列
(2)∵a1=2,b1=2
∴由①得a2=6,再由②得b2=3
等差数列{bn}的首项b1=2公差 d=b2-b1=1∴bn=2+(n-1)=n+1
当n≥2时,an=bn-1bn=n(n+1),当n=1时,a1=2也成立
∴数列{an}通项公式为an=n(n+1)
∴
| 1 |
| an |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
数列{
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
∴Sn<1
点评:(1)等差数列的证明常用的方法(i)定义法:an-an-1=d;(ii)等差中项法:2an=an-1+an+1
(2)裂项求和是数列求和中的重要方法,要注意其适用的结构特点
(2)裂项求和是数列求和中的重要方法,要注意其适用的结构特点

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 (2011•甘肃一模)某高中共有学生2000名,各年级男、女生人数如表所示.已知在全校学生中随机抽取1名,抽到高三年级男生的概率是0.16,现用分层抽样的方法在全校抽取64名学生,则应在高一年级抽取的学生人数为( )
(2011•甘肃一模)某高中共有学生2000名,各年级男、女生人数如表所示.已知在全校学生中随机抽取1名,抽到高三年级男生的概率是0.16,现用分层抽样的方法在全校抽取64名学生,则应在高一年级抽取的学生人数为( )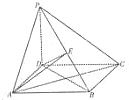 (2011•甘肃一模)如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD=1.
(2011•甘肃一模)如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD=1.