Question

直线y=1与曲线y=x²-|x|+a有两个交点，则a的取值范围是

a＜1或a=

5

4

．

Answer 1

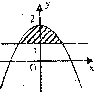
分析：先画出函数的图象，根据已知条件即可求出a的取值范围．

解答：解：∵曲线y=x²-|x|+a=

(x- 1 2 )2+a- 1 4 ，当x≥0时 (x+ 1 2 )2+a- 1 4 ，当x＜0时

，作出函数图象：
由图象可知：若使直线y=1与曲线y=x²-|x|+a有两个交点，
则满足a＜1或a-

1

4

=1，
故答案为a＜1或a=

5

4

．

点评：熟练掌握二次函数的图象和性质是解题的关键．