Question

直线y=1与曲线y=x²-|x|+a有四个交点，则实数a的取值范围是（　　）

Answer 1

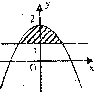
分析：直线y=1与曲线y=x²-|x|+a有四个交点?函数y=1-a与函数y=x²-|x|的图象由四个不同的交点，画出图象即可得出．

解答：解：分别作出函数y=1-a，y=x²-|x|=

(x- 1 2 )2- 1 4 ，当x≥0时 (x+ 1 2 )2- 1 4 ，当x＜0时

的图象，
由图象可知：函数y=x²-|x|的值域为[-

1

4

，+∞)，
要使函数y=1-a与函数y=x²-|x|的图象由四个不同的交点，则a必须满足-

1

4

＜1-a＜0，
解得1＜a＜

5

4

，即直线y=1与曲线y=x²-|x|+a有四个交点．
故选D．

点评：熟练掌握函数的奇偶性、单调性及数形结合是解题的关键．