题目内容
直线y=1与曲线y=x2-|x|+a有四个交点，则a的取值范围是分析：在同一直角坐标系内画出直线y=1与曲线y=x2-|x|+a的图象，观察求解．
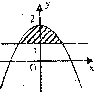
解答：
解：如图，在同一直角坐标系内画出直线y=1与曲线y=x2-|x|+a，
观图可知，a的取值必须满足
，
解得1＜a＜
．
故答案为：（1，
）
解：如图，在同一直角坐标系内画出直线y=1与曲线y=x2-|x|+a，观图可知，a的取值必须满足
|
解得1＜a＜
| 5 |
| 4 |
故答案为：（1，
| 5 |
| 4 |
点评：本小题主要考查函数的图象与性质、不等式的解法，着重考查了数形结合的数学思想．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
