题目内容
已知数列{ an}的前n项和为Sn,且Sn=2an-l;数列{bn}满足bn-1-bn=bnbn-1(n≥2,n∈N*)b1=1.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)求数列{ }的前n项和T.
}的前n项和T.
解:(Ⅰ)当n=1时,a1=S1=2a1-1,解得a1=1.
又当n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1)=2an-2an-1,
∴an=2an-1(n≥2).
∴数列{an}是首项为1,公比为2的等比数列.
∴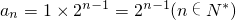 .
.
由bn-1-bn=bnbn-1,得 .
.
又b1=1,所以数列{ }是首项为
}是首项为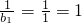 ,公差为1的等差数列.
,公差为1的等差数列.
∴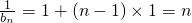 .
.
∴ .
.
(Ⅱ)由(Ⅰ)可得: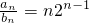 ,
,
∴Tn=1×20+2×21+…+n•2n-1,
2Tn=1×21+2×22+…+(n-1)•2n-1+n•2n,.
两式相减,得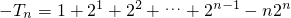 =
=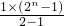 -n•2n=2n-1-n•2n.
-n•2n=2n-1-n•2n.
∴ .
.
分析:(Ⅰ)利用 即可得出an,由bn-1-bn=bnbn-1,两边同除以bnbn-1得
即可得出an,由bn-1-bn=bnbn-1,两边同除以bnbn-1得 ,进而利用得出数列的通项公式即可得出..
,进而利用得出数列的通项公式即可得出..
(Ⅱ)由(Ⅰ)可得: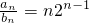 ,再利用“错位相减法”即可得出Tn.
,再利用“错位相减法”即可得出Tn.
点评:数列掌握公式 、由bn-1-bn=bnbn-1,两边同除以bnbn-1转化为等差数列问题、“错位相减法”是解题的关键.
、由bn-1-bn=bnbn-1,两边同除以bnbn-1转化为等差数列问题、“错位相减法”是解题的关键.
又当n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1)=2an-2an-1,
∴an=2an-1(n≥2).
∴数列{an}是首项为1,公比为2的等比数列.
∴
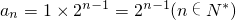 .
.由bn-1-bn=bnbn-1,得
 .
.又b1=1,所以数列{
 }是首项为
}是首项为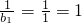 ,公差为1的等差数列.
,公差为1的等差数列.∴
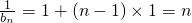 .
.∴
 .
.(Ⅱ)由(Ⅰ)可得:
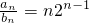 ,
,∴Tn=1×20+2×21+…+n•2n-1,
2Tn=1×21+2×22+…+(n-1)•2n-1+n•2n,.
两式相减,得
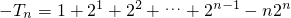 =
=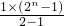 -n•2n=2n-1-n•2n.
-n•2n=2n-1-n•2n.∴
 .
.分析:(Ⅰ)利用
 即可得出an,由bn-1-bn=bnbn-1,两边同除以bnbn-1得
即可得出an,由bn-1-bn=bnbn-1,两边同除以bnbn-1得 ,进而利用得出数列的通项公式即可得出..
,进而利用得出数列的通项公式即可得出..(Ⅱ)由(Ⅰ)可得:
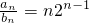 ,再利用“错位相减法”即可得出Tn.
,再利用“错位相减法”即可得出Tn.点评:数列掌握公式
 、由bn-1-bn=bnbn-1,两边同除以bnbn-1转化为等差数列问题、“错位相减法”是解题的关键.
、由bn-1-bn=bnbn-1,两边同除以bnbn-1转化为等差数列问题、“错位相减法”是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目