题目内容
【题目】已知公差为0的等差数列{an}满足a1=1，且a1 ， a3﹣2，a9成等比数列．
（1）求数列{an}的通项公式；
（2）记数列{ 
}的前n项和为Sn ， 并求使得Sn＞ 
+ 
成立的最小正整数n．
【答案】
（1）解：设数列{an}的公差为d，
由a1，a3﹣2，a9成等比数列得，（2d﹣1）2=1×（1+8d），
则d2﹣3d=0，解得d=3或d=0（舍去），
所以an=1+（n﹣1）d=3n﹣2；
（2）解：由（1）得， 
= 
= 
（ 
），
则Sn= [（1﹣ 
）+（ 
）+…+（ ）]
= （ 
）= 
，
所以Sn＞ 
+ 为 ＞ + ，化简得，
n2﹣25n﹣8＞0，又n是正整数，解得n≥26，
所以Sn= ，使得Sn＞ + 成立的最小正整数n为26
【解析】（1）设数列{an}的公差为d，根据等比中项的性质、等差数列的通项公式列出方程，求出d的值，代入等差数列的通项公式求出an；（2）由（1）化简 ，利用裂项相消法求出Sn ， 化简Sn＞ + 求出n的范围，即可求出最小正整数n．
【考点精析】通过灵活运用等差数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：
或
；数列{an}的前n项和sn与通项an的关系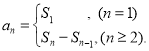
即可以解答此题．
练习册系列答案
相关题目
