题目内容
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,高AA1=2,求:(1)异面直线BD与AB1所成的角的大小的余弦值
(2)四面体AB1D1C的体积.
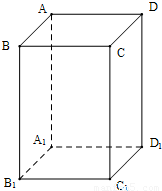
【答案】分析:(1)根据题意知DC1∥AB1∴∠BDC1就是异面直线BD 与AB1 所成角,解三角形即可求得结果.
(2)VA-B1D1C=VABCD-A1B1C1D1-VB1-ABC-VD1-ACD-VDA1C1D1-VB-A1B1C1,而VABCD-A1B1C1D1-VB1-ABC-VD1-ACD-VDA1C1D1-VB-A1B1C1易求,即可求得四面体AB1D1C 的体积.
解答: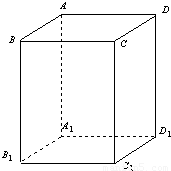 解:(1)连接DC1,BC1,
解:(1)连接DC1,BC1,
易知DC1∥AB1,
∴∠BDC1就是异面直线BD 与AB1 所成角,
在△BDC1中,DC1=BC1=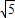 ,BD=
,BD=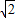 ,
,
∴cos∠BDC1=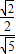 =
=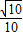 .
.
所以异面直线BD与AB1所成的角的大小的余弦值为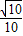 .
.
(2)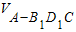 =
=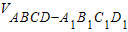 -
-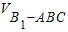 -
-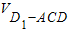 -
-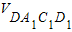 -
-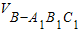
而VABCD-AB1C1D1=SABCD•AA1=1×2=2,
VB1-ABC=VD1-ACD=VDA1C1D1=VB-A1B1C1= ×
× ×2.
×2.
∴VA-B1D1C═2-4× ×
× ×2=
×2= .
.
所以四面体AB1D1C的体积为 .
.
点评:此题是个基础题.考查异面直线所成角和棱锥的体积问题,求解方法一般是平移法,转化为平面角问题来解决,和利用割补法求棱锥的体积问题,体现了数形结合和转化的思想.
(2)VA-B1D1C=VABCD-A1B1C1D1-VB1-ABC-VD1-ACD-VDA1C1D1-VB-A1B1C1,而VABCD-A1B1C1D1-VB1-ABC-VD1-ACD-VDA1C1D1-VB-A1B1C1易求,即可求得四面体AB1D1C 的体积.
解答:
 解:(1)连接DC1,BC1,
解:(1)连接DC1,BC1,易知DC1∥AB1,
∴∠BDC1就是异面直线BD 与AB1 所成角,
在△BDC1中,DC1=BC1=
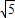 ,BD=
,BD=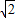 ,
,∴cos∠BDC1=
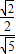 =
=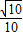 .
.所以异面直线BD与AB1所成的角的大小的余弦值为
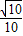 .
.(2)
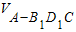 =
=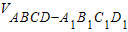 -
-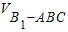 -
-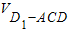 -
-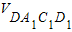 -
-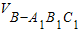
而VABCD-AB1C1D1=SABCD•AA1=1×2=2,
VB1-ABC=VD1-ACD=VDA1C1D1=VB-A1B1C1=
 ×
× ×2.
×2.∴VA-B1D1C═2-4×
 ×
× ×2=
×2= .
.所以四面体AB1D1C的体积为
 .
.点评:此题是个基础题.考查异面直线所成角和棱锥的体积问题,求解方法一般是平移法,转化为平面角问题来解决,和利用割补法求棱锥的体积问题,体现了数形结合和转化的思想.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 已知正方体ABCD-A1B1C1D1的棱长为a,
已知正方体ABCD-A1B1C1D1的棱长为a, 如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1,
如图所示,已知在正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,E为C1C上的点,且CE=1, 如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点.
如图:已知正方体ABCD-A1B1C1D1中,点F为A1D的中点. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.