Question

如图所示，已知在正四棱柱ABCD-A₁B₁C₁D₁中，底面边长AB=2，侧棱BB₁的长为4，E为C₁C上的点，且CE=1，
（1）求证：A₁C⊥平面BDE；
（2）求A₁B与平面BDE所成的角的正弦值．

Answer 1

分析：（1）建立空间直角坐标系，利用向量的数量积，可证得直线A₁C与BE，BD均垂直，再由线面垂直的判定定理得到A₁C⊥平面BED；
（2）由（1）中结论，我们可得

A1C

是平面BDE的一个法向量，再求出直线A₁B的方向向量，代入向量夹角公式，即可得到A₁B与平面BDE所成角的正弦值的大小．

解答：（1）证明：以D为原点，DA、DC、DD₁所在直线分别为x、y、z轴建立空间直角坐标系D-xyz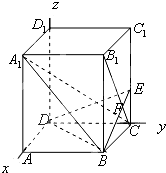
则D（0，0，0），A（2，0，0），B（2，2，0），C（0，2，0），A₁（2，0，4），B₁（2，2，4），C₁（0，2，4），D₁（0，0，4），E（0，2，1），
∴

BE

=（-2，0，1）．
∵

A1C

=（-2，2，-4），

DB

=（2，2，0），
∴

A1C

•

BE

=4+0-4=0且

A1C

•

DB

=-4+4+0=0，
∴

A1C

⊥

DB

且

A1C

⊥

BE

，
∵DB∩BE=B
∴A₁C⊥平面BDE；                  
（2）解：由（1）知

A1C

=（-2，2，-4）是平面BDE的一个法向量，
∵

A1B

=（0，2，-4），
∴cos＜

A1C

，

A1B

＞=

A1C • A1B

| A1C || A1B |

=

30

6

，
∴A₁B与平面BDE所成角的正弦值为

30

6

．

点评：本题考查的知识点是用空间向量求直线与平面的夹角，向量语言表述线面的垂直、平行关系，其中建立空间坐标系，将空间线面的夹角及垂直、平行问题转化为向量夹角问题是解答此类问题的关键．