题目内容
如图，已知平面BCC1B1是圆柱的轴截面（经过圆柱的轴的截面），BC是圆柱底面的直径，O为底面圆心，E为母线CC1的中点，已知AB=AC=AA1=4，
（Ⅰ）求证：B1O⊥平面AEO；
（Ⅱ）求二面角B1-AE-O的余弦值。
（Ⅰ）求证：B1O⊥平面AEO；
（Ⅱ）求二面角B1-AE-O的余弦值。
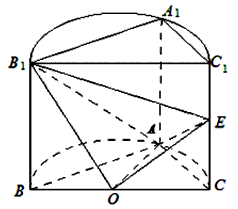
| 解：依题意可知，AA1⊥平面ABC，∠BAC=90°， 如图建立空间直角坐标系A-xyz， 因为  =4，则  ，（Ⅰ）  ， ，∴  ，∴B1O⊥EO，  ， ∴  ，∵AO∩EO=O，  ，∴  ；（Ⅱ）平面AEO的法向量为  ，设平面B1AE的法向量为  ，∴  ，令x=2，则z=-2，y=1， ∴  ，∴  ，∴二面角B1-AE-F的余弦值为  。 |
 |
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
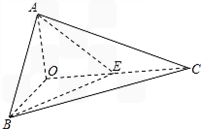
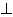底面BCDE，BC=2，
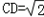，AB=AC．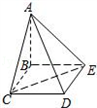 
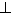CE；
，SB=2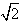
，
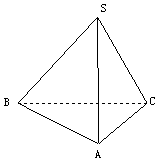
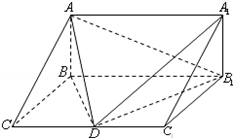
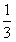，AC=BC=AA1时，求二面角C1-AB-C的大小。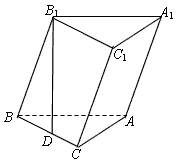 
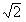，侧棱AA1=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M，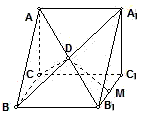 
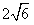，则侧面与底面所成的二面角的平面角为（ ）。