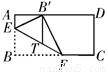
题目内容
如图9,有一根长为
图9
解:如图,把圆柱表面及缠绕其上的铁丝展开在平面上,得到矩形ABCD.
由题意,知BC=
故线段AC的长度即为铁丝的最短长度.
∴AC=![]() ≈27.05(cm).
≈27.05(cm).
∴铁丝的最短长度约为
点评:此题关键是把圆柱沿这条母线展开,将问题转化为平面几何问题.探究几何体表面上最短距离,常将几何体的表面或侧面展开,化折(曲)为直,使空间图形问题转化为平面图形问题.空间问题平面化是解决立体几何问题基本的、常用的方法.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
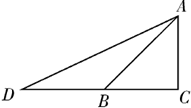 如图,有一条长为a的斜坡AB,它的坡角∠ABC=45°,现保持坡高AC不变,将坡角改为∠ADC=30°,则斜坡AD的长为( )
如图,有一条长为a的斜坡AB,它的坡角∠ABC=45°,现保持坡高AC不变,将坡角改为∠ADC=30°,则斜坡AD的长为( )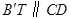 交EF于点T,求点T的轨迹方程.
交EF于点T,求点T的轨迹方程.