Question

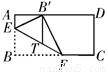
如图，有一张长为8，宽为4的矩形纸片ABCD，按图示的方向进行折叠，使每次折叠后点B都落在AD边上，此时将B记为B′（图中EF为折痕，点F也可以落在边CD上）．过B′作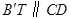交EF于点T，求点T的轨迹方程．

 

Answer 1

【答案】

．

【解析】

试题分析：解：如图，以边的中点为原点，边所在的直线为轴建立平面直角坐标系，则．

因为，，根据抛物线的定义，点的轨迹是以点为焦点，为准线的抛物线的一部分．

设，由，即定点到定直线的距离为4．

设，由，即定点到定直线的距离为4．

所以抛物线的方程为．

在折叠中，线段长度在区间内变化，而，所以．

故点的轨迹方程为．

考点：本题主要考查抛物线的定义及标准方程。

点评：基础题，分析图形的几何性质，联想定义是关键，易错点是忽视x的变化范围。