题目内容
设φ∈R,则“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:由“φ=0”可以推出“f(x)=cos(x+φ)=cosx (x∈R)为偶函数”,所以是充分的,再由“f(x)=cos(x+φ)(x∈R)为偶函数”可以推出 ,并不一定有φ=0,所以不必要;因此“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的充分而不必要条件;故选A.
,并不一定有φ=0,所以不必要;因此“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的充分而不必要条件;故选A.
考点:充要条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题p: x∈R,x2+x-6
x∈R,x2+x-6 0,则命题
0,则命题 P是( )
P是( )
A. x∈R,x2+x-6>0 x∈R,x2+x-6>0 | B. x∈R.x2+x-6>0 x∈R.x2+x-6>0 |
C. x∈R,x2+x-6>0 x∈R,x2+x-6>0 | D. x∈R.x2+x-6<0 x∈R.x2+x-6<0 |
设函数 条件
条件 :“
:“ ”;条件
”;条件 :“
:“ 为奇函数”,则
为奇函数”,则 是
是 的 ( ).
的 ( ).
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
以下有关命题的说法错误的是( )
A.命题“若 则x=1”的逆否命题为“若 则x=1”的逆否命题为“若 ” ” |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.若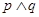 为假命题,则p、q均为假命题 为假命题,则p、q均为假命题 |
D.对于命题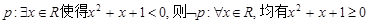 |
已知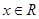 ,则“
,则“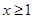 ”是“
”是“ ”的( ).
”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 则
则 是( ).
是( ).
A. | B. |
C. | D. |
“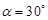 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在 中,角
中,角 、
、 、
、 所对应的变分别为
所对应的变分别为 、
、 、
、 ,则
,则 是
是 的( )
的( )
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
 ,
, ,全集为R
,全集为R 时,求:
时,求: ;
; ,求实数
,求实数 的取值范围.
的取值范围.  时,求B的非空真子集的个数;
时,求B的非空真子集的个数;