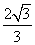题目内容
已知实数 (
( )满足
)满足 ,记
,记 .
.
(Ⅰ)求 及
及 的值;
的值;
(Ⅱ)当 时,求
时,求 的最小值;
的最小值;
(Ⅲ)求 的最小值.
的最小值.
注: 表示
表示 中任意两个数
中任意两个数 ,
, (
( )的乘积之和.
)的乘积之和.
解:(Ⅰ)由已知得 .
.
 .
.
(Ⅱ)设 .
.
当 时,
时, .
.
若固定 ,仅让
,仅让 变动,此时
变动,此时 ,
,
因此 .
.
同理 .
.
 .
.
以此类推,我们可以看出, 的最小值必定可在某一组取值
的最小值必定可在某一组取值 的
的 所达到,
所达到,
于是 .
.
当 (
( )时,
)时,
 .
.
因为 ,所以
,所以 ,且当
,且当 ,
, 时,
时, .
.
因此 .
.
(Ⅲ)设
 .
.
固定 ,仅让
,仅让 变动,此时
变动,此时
 ,
,
因此 .
.
同理 .
.
 .
.
以此类推,我们可以看出, 的最小值必定可在某一组取值
的最小值必定可在某一组取值 的
的 所达到,于是
所达到,于是 .
.
当 (
( )时,
)时,
 .
.
①当 为偶数时,
为偶数时, ,
,
若取 ,
, ,则
,则 ,所以
,所以 .
.
②当 为奇数时,因为
为奇数时,因为 ,所以
,所以 ,
,
若取 ,
, ,则
,则 ,
,
所以 .
.

练习册系列答案
相关题目
 中,
中, 等于( )
等于( ) 上到直线
上到直线 的距离为
的距离为 的点的个数是 _ .
的点的个数是 _ .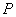 是棱长为1的正方体
是棱长为1的正方体 的底面
的底面 上一点,则
上一点,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 中,
中,  所对的边分别为
所对的边分别为 ,且
,且
 .
. 的最大值;
的最大值; ,求b的值.
,求b的值. ,抛物线
,抛物线 的焦点是
的焦点是 ,若抛物线上存在一点
,若抛物线上存在一点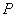 ,使得
,使得 最小,则
最小,则 (B)
(B) (C)
(C) (D)
(D)
 的图象为
的图象为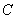 ,有如下结论:①图象
,有如下结论:①图象 对称;②图象
对称;②图象 对称;③函数
对称;③函数 在区间
在区间 内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号)
内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号) 与点
与点 重合,
重合, 重合的点是
重合的点是 B.
B. C.
C. D.
D.
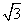 的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )
的球面上,若PA、PB、PC两两互相垂直,则球心到截面ABC的距离为( )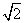 B.
B. 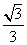 D.
D.