题目内容
【题目】在四面体S﹣ABC中, ![]() ,二面角S﹣AC﹣B的余弦值为-
,二面角S﹣AC﹣B的余弦值为- ![]() ,则该四面体外接球的表面积是( )
,则该四面体外接球的表面积是( )
A.![]()
B.![]()
C.24π
D.6π
【答案】D
【解析】解:取AC中点D,连接SD,BD, 因为AB=BC= ![]() ,所以BD⊥AC,
,所以BD⊥AC,
因为SA=SC=2,所以SD⊥AC,AC⊥平面SDB.
所以∠SDB为二面角S﹣AC﹣B.
在△ABC中,AB⊥BC,AB=BC= ![]() ,
,
所以AC=2.
取等边△SAC的中心E,作EO⊥平面SAC,
过D作DO⊥平面ABC,O为外接球球心,
所以ED= ![]() ,二面角S﹣AC﹣B的余弦值是﹣
,二面角S﹣AC﹣B的余弦值是﹣ ![]() ,所以cos∠EDO=
,所以cos∠EDO= ![]() ,OD=
,OD= ![]() ,
,
所以BO= ![]() =OA=OS=OC
=OA=OS=OC
所以O点为四面体的外接球球心,
其半径为 ![]() ,表面积为6π.
,表面积为6π.
故选:D.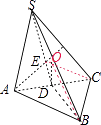

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
