题目内容
若无穷数列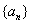 满足:①对任意
满足:①对任意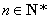 ,
,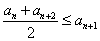 ;②存在常数
;②存在常数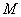 ,对任意
,对任意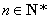 ,
,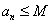 ,则称数列
,则称数列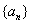 为“
为“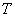 数列”.
数列”.
(Ⅰ)若数列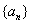 的通项为
的通项为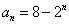
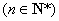 ,证明:数列
,证明:数列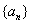 为“
为“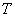 数列”;
数列”;
(Ⅱ)若数列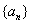 的各项均为正整数,且数列
的各项均为正整数,且数列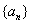 为“
为“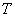 数列”,证明:对任意
数列”,证明:对任意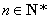 ,
,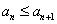 ;
;
(Ⅲ)若数列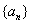 的各项均为正整数,且数列
的各项均为正整数,且数列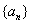 为“
为“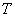 数列”,证明:存在
数列”,证明:存在 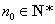 ,数列
,数列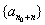 为等差数列.
为等差数列.
(Ⅰ)证明:由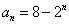 ,可得
,可得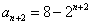 ,
,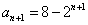 ,
,
所以 ,
,
所以对任意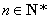 ,
,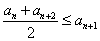 .
.
又数列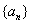 为递减数列,所以对任意
为递减数列,所以对任意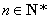 ,
,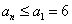 .
.
所以数列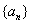 为“
为“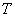 数列”.
数列”.
(Ⅱ)证明:假设存在正整数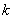 ,使得
,使得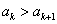 .
.
由数列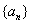 的各项均为正整数,可得
的各项均为正整数,可得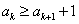 .
.
由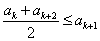 ,可得
,可得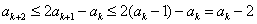 .
.
且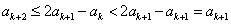 .
.
同理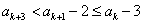 ,
,
依此类推,可得,对任意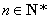 ,有
,有 .
.
因为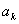 为正整数,设
为正整数,设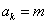 ,则
,则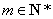 .
.
在 中,设
中,设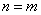 ,则
,则 .
.
与数列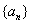 的各项均为正整数矛盾.
的各项均为正整数矛盾.
所以,对任意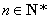 ,
,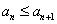 .
.
(Ⅲ)因为数列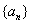 为“
为“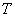 数列”,
数列”,
所以,存在常数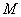 ,对任意
,对任意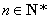 ,
,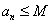 .
.
设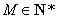 .
.
由(Ⅱ)可知,对任意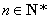 ,
,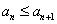 ,
,
则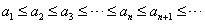 .
.
若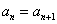 ,则
,则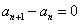 ;若
;若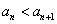 ,则
,则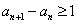 .
.
而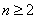 时,有
时,有 .
.
所以 ,
,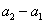 ,
,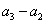 ,…,
,…,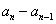 ,…,中最多有
,…,中最多有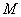 个大于或等于
个大于或等于 ,
,
否则与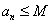 矛盾.
矛盾.
所以,存在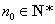 ,对任意的
,对任意的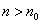 ,有
,有 .
.
所以,对任意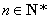 ,
,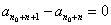 .
.
所以,存在 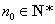 ,数列
,数列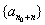 为等差数列.
为等差数列.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 (y≠0) B.
(y≠0) B.  (y≠0)
(y≠0)  (y≠0) D.
(y≠0) D. 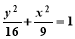 (y≠0)
(y≠0)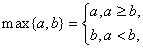 设实数
设实数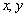 满足约束条件
满足约束条件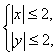 则
则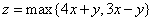 的取值范围是
的取值范围是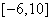 (B)
(B)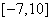 (C)
(C)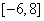 (D)
(D)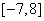
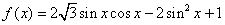 .
.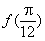 的值;
的值;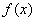 在区间
在区间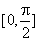 上的最大值和最小值.
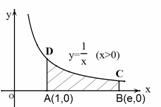
上的最大值和最小值.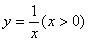 ,e是自然对数的底,则曲边梯形的面积是
,e是自然对数的底,则曲边梯形的面积是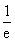 (D)
(D)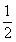
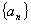 的首项
的首项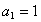 ,前三项之和
,前三项之和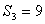 ,则
,则 .
. 与圆
与圆 相切于点
相切于点 ,过点
,过点 作圆
作圆 于
于 两点,
两点, ,
, ,则圆
,则圆