题目内容
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 不是
不是 的直径,
的直径, 的中点为
的中点为 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)由圆的内接四边形的性质得 ,由等腰三角形的性质得
,由等腰三角形的性质得 ,则有
,则有 ,充分挖掘角的等量关系是解题关键;(Ⅱ)要证明
,充分挖掘角的等量关系是解题关键;(Ⅱ)要证明 为等边三角形,只需证明三个内角相等.由
为等边三角形,只需证明三个内角相等.由 得,需证
得,需证 ,故只需证明
,故只需证明 .由
.由 得,
得, 在弦
在弦 的垂直平分线上,该直线必然是直径所在的直线,又
的垂直平分线上,该直线必然是直径所在的直线,又 是非直径的弦
是非直径的弦 的中点,故该直线垂直于
的中点,故该直线垂直于 ,则
,则 ,进而证明
,进而证明 为等边三角形.
为等边三角形.
试题解析:(I)由题设知 四点共圆,所以
四点共圆,所以 .由已知得
.由已知得 ,故
,故 .
.
(II)设 的中点为
的中点为 ,连接
,连接 ,则由
,则由 知
知 ,故
,故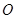 在直线
在直线 上.又
上.又 不是
不是 的直径,
的直径, 的中点为
的中点为 ,故
,故 ,即
,即 .所以
.所以 ,故
,故 .又
.又 ,故
,故 .由(1)知,
.由(1)知, ,所以
,所以 为等边三角形.
为等边三角形.
【考点定位】1、圆的内接四边形的性质;2、垂径定理的推论.

练习册系列答案
相关题目
 是⊙
是⊙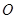 直径,弦
直径,弦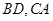 的延长线交于
的延长线交于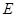 ,
,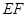 垂直于
垂直于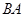 的延长线于
的延长线于 .求证:
.求证: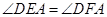 ;
;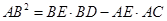 .
.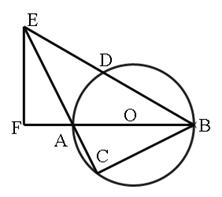
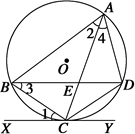


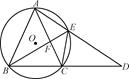


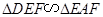 ;(2)EF//CB.
;(2)EF//CB. 是
是 的外接圆,过点
的外接圆,过点 的切线交
的切线交 的延长线于点
的延长线于点 ,
, ,则
,则 的长为 .
的长为 .