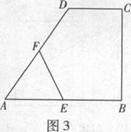
题目内容
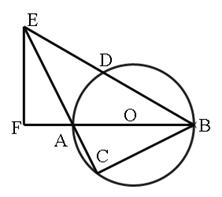
如图所示, 是⊙
是⊙ 直径,弦
直径,弦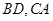 的延长线交于
的延长线交于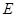 ,
,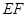 垂直于
垂直于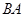 的延长线于
的延长线于 .求证:
.求证:
(1)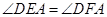 ;
;
(2)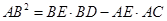 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)分析结论成立所需条件,拉近它与已知条件的距离,要熟悉圆所具有的一切性质,和四点共圆所需条件,这是解决此题的前提;(2)要熟悉圆所具有的一切性质,注意比例式与乘积式的转化,掌握常规问题的处理方法.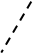

试题解析: (1)连接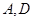 ,连接
,连接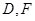 ,因为
,因为 是⊙
是⊙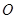 直径,所以
直径,所以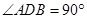 ,从而
,从而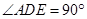
又因为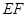 垂直于
垂直于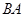 的延长线于
的延长线于 ,所以
,所以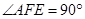 ,因此
,因此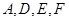 四点共圆,根据同弧所对的圆周角相等,可得劣弧
四点共圆,根据同弧所对的圆周角相等,可得劣弧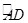 所对的圆周角
所对的圆周角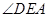 与
与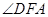 相等,即
相等,即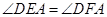 . 5分
. 5分
(2)因为 是⊙
是⊙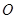 直径,所以
直径,所以 ,即
,即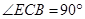 又因为
又因为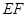 垂直于
垂直于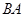 的延长线于
的延长线于 ,所以
,所以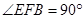 ,因此
,因此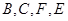 四点共圆,根据相交线定理有:
四点共圆,根据相交线定理有: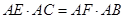 ①
①
在△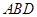 和△
和△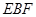 中,有
中,有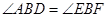 ,
,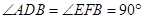 ,因此△
,因此△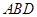 ∽△
∽△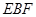 ,从而有
,从而有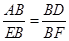 ,即
,即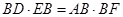 ②
②
由①②得: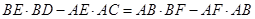
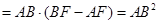 ,
,
即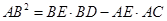 得证. 10分
得证. 10分
考点:平面几何中圆与三角形的知识.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 PEC=
PEC=  PF的值
PF的值
 的直径
的直径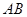 的长为4,点
的长为4,点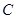 平分弧
平分弧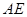 ,过
,过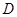 ,交
,交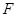 .
.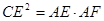 :
: 的角平分线,求
的角平分线,求 的长.
的长.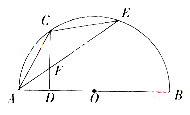
 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
 ;
; 不是
不是 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形. 是⊙
是⊙ 的一条弦,点
的一条弦,点 为
为 ,
, 交⊙
交⊙ ,若
,若 ,
, ,则
,则
 ,且满足
,且满足 则
则 .
.
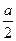 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .