题目内容
已知四面体S-ABC各棱长都为1，则棱SA与平面ABC所成的角的余弦值为分析：设四面体 的棱长为a，过S作SM⊥平面ABC，垂足为M，则M为三角形ABC的中心，则可得∠SAM即为直线与平面所成的角
在Rt△SAM中，cos∠SAM=
可求
在Rt△SAM中，cos∠SAM=
| AM |
| AS |
解答：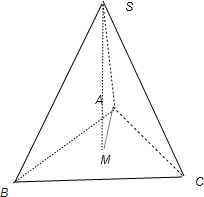
解：设四面体 的棱长为a，过S作SM⊥平面ABC，垂足为M，
则M为三角形ABC的中心，
连接AM，则可得∠SAM即为直线与平面所成的角
在Rt△SAM中，可知SA=a，AM=
×
a=
a，cos∠SAM=
=
∴∠SAM=arccos
故答案为：arccos
解：设四面体 的棱长为a，过S作SM⊥平面ABC，垂足为M，则M为三角形ABC的中心，
连接AM，则可得∠SAM即为直线与平面所成的角
在Rt△SAM中，可知SA=a，AM=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| AM |
| AS |
| ||
| 3 |
∴∠SAM=arccos
| ||
| 3 |
故答案为：arccos
| ||
| 3 |
点评：本题主要考查了直线与平面所成的角的求解，解题的关键是要找到已知平面的垂线，进而找出所要求解的线面角，然后转化为在（直角）三角形中进行求解．
练习册系列答案
相关题目
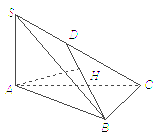已知四面体S－ABC中，SA⊥底面ABC，△ABC是锐角三角形，H是点A在面SBC上的射影．求证：H不可能是△SBC的垂心．