题目内容
(本小题满分10分)选修4-5:不等式选讲
已知 ,不等式
,不等式 的解集为
的解集为 .
.
(1)求 ;
;
(2)当 时,证明:
时,证明: .
.
(1) ;(2)证明见解析
;(2)证明见解析
【解析】
试题分析:(1)理解绝对值的几何意义, 表示的是数轴的上点
表示的是数轴的上点 到原点离.(2)对于恒成立的问题,常用到以下两个结论:(1)
到原点离.(2)对于恒成立的问题,常用到以下两个结论:(1) 恒成立
恒成立 ,(2)
,(2) 恒成立
恒成立
(3)掌握一般不等式的解法: 或
或 ,
, .
.
试题解析:(1)解不等式: ;(4)逆向思维是用分析法证题的主要思想,通过反推,逐步寻找使结论成立的充分条件,正确把握转化方向是使问题顺利获解的关键.
;(4)逆向思维是用分析法证题的主要思想,通过反推,逐步寻找使结论成立的充分条件,正确把握转化方向是使问题顺利获解的关键.
 或
或 或
或

 或
或 或
或 ,
,



 .
.
(2)需证明: ,
,
只需证明 ,
,
即需证明
证明: 

 ,所以原不等式成立.
,所以原不等式成立.
考点:1、含绝对值不等式的解法;2、证明不等式.
考点分析: 考点1:含绝对值的不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,若
,若 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
 上存在点
上存在点 满足约束条件
满足约束条件 则实数
则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的外接圆半径为1,圆心为
的外接圆半径为1,圆心为 ,且
,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,则输出
,则输出 的值为( )
的值为( )
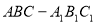 中,
中,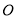 是
是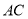 的中点,
的中点,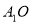 ⊥平面
⊥平面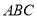 ,
, ,
,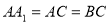 .
. 
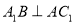 ;
;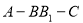 的余弦值.
的余弦值.  的外接圆半径为1,圆心为
的外接圆半径为1,圆心为 ,且
,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 与曲线
与曲线 有四个不同交点,则实数
有四个不同交点,则实数 的取值范围是 ( ).
的取值范围是 ( ). B.
B. C.
C. D.
D.
 的反函数为 .
的反函数为 .