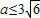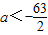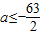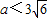题目内容
已知函数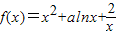 在(1,4)上是减函数,则实数a的取值范围是( )
在(1,4)上是减函数,则实数a的取值范围是( )A.
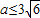
B.
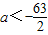
C.
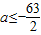
D.
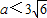
【答案】分析:求出原函数的导函数,由函数 在(1,4)上是减函数得其导函数在x∈(1,4)时小于等于0恒成立,分离变量后再利用导数分析单调性,从而求出a的范围.
在(1,4)上是减函数得其导函数在x∈(1,4)时小于等于0恒成立,分离变量后再利用导数分析单调性,从而求出a的范围.
解答:解:由 ,得
,得 ,
,
因为 在(1,4)上是减函数,
在(1,4)上是减函数,
所以当x∈(1,4)时,2x3+ax-2≤0恒成立,
即 在x∈(1,4)时恒成立,
在x∈(1,4)时恒成立,
令 ,则
,则 ,
,
所以 在x∈(1,4)上为减函数,此时
在x∈(1,4)上为减函数,此时 .
.
所以 .
.
故选C.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,考查了分离变量法求函数的最值,是中档题.
 在(1,4)上是减函数得其导函数在x∈(1,4)时小于等于0恒成立,分离变量后再利用导数分析单调性,从而求出a的范围.
在(1,4)上是减函数得其导函数在x∈(1,4)时小于等于0恒成立,分离变量后再利用导数分析单调性,从而求出a的范围.解答:解:由
 ,得
,得 ,
,因为
 在(1,4)上是减函数,
在(1,4)上是减函数,所以当x∈(1,4)时,2x3+ax-2≤0恒成立,
即
 在x∈(1,4)时恒成立,
在x∈(1,4)时恒成立,令
 ,则
,则 ,
,所以
 在x∈(1,4)上为减函数,此时
在x∈(1,4)上为减函数,此时 .
.所以
 .
.故选C.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系,考查了分离变量法求函数的最值,是中档题.

练习册系列答案
相关题目
 在(1,4)上是减函数,则实数
在(1,4)上是减函数,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
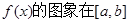 上连续不断,定义:
上连续不断,定义: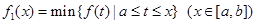 ,
,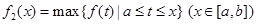 ,其中,
,其中,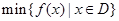 表示函数
表示函数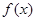 在
在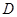 上的最小值,
上的最小值,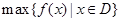 表示函数
表示函数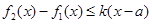 对任意的
对任意的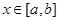 成立,则称函数
成立,则称函数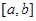 上的“
上的“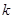 阶收缩函数” .
阶收缩函数” .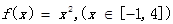 为[-1,4]上的“
为[-1,4]上的“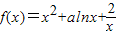 在(1,4)上是减函数,则实数a的取值范围是( )
在(1,4)上是减函数,则实数a的取值范围是( )