题目内容
已知曲线y=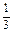 x3+
x3+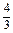 .
.
(1)求曲线在x=2处的切线方程;
(2)求曲线过点(2,4)的切线方程.
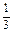 x3+
x3+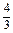 .
.(1)求曲线在x=2处的切线方程;
(2)求曲线过点(2,4)的切线方程.
(1)4x-y-4=0(2)切线方程为4x-y-4=0或x-y+2=0
(1)∵y′=x2,
∴在点P(2,4)处的切线的斜率k=y′|x=2="4. " 3分
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),
即4x-y-4="0. " 6分
(2)设曲线y=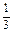 x3+
x3+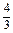 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点
A(x0,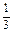 x03+
x03+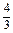 ),则切线的斜率
),则切线的斜率
k=y′|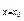 =x02. 8分
=x02. 8分
∴切线方程为y-(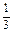 x03+
x03+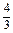 )=x02(x-x0),
)=x02(x-x0),
即y=x02·x-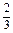 x03+
x03+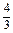 . 10分
. 10分
∵点P(2,4)在切线上,∴4=2x02-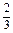 x03+
x03+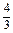 ,
,
即x03-3x02+4=0,∴x03+x02-4x02+4=0,
∴x02 (x0+1)-4(x0+1)(x0-1)=0,
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2="0. " 14分
∴在点P(2,4)处的切线的斜率k=y′|x=2="4. " 3分
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),
即4x-y-4="0. " 6分
(2)设曲线y=
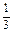 x3+
x3+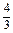 与过点P(2,4)的切线相切于点
与过点P(2,4)的切线相切于点A(x0,
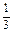 x03+
x03+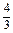 ),则切线的斜率
),则切线的斜率k=y′|
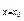 =x02. 8分
=x02. 8分∴切线方程为y-(
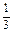 x03+
x03+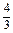 )=x02(x-x0),
)=x02(x-x0),即y=x02·x-
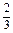 x03+
x03+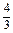 . 10分
. 10分∵点P(2,4)在切线上,∴4=2x02-
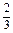 x03+
x03+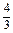 ,
,即x03-3x02+4=0,∴x03+x02-4x02+4=0,
∴x02 (x0+1)-4(x0+1)(x0-1)=0,
∴(x0+1)(x0-2)2=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2="0. " 14分

练习册系列答案
相关题目
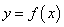 ,若同时满足
,若同时满足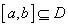 ,使得任取
,使得任取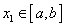 ,都有
,都有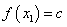 (
(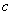 是常数);
是常数);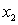 ,当
,当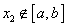 时总有
时总有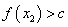 ;
;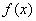 为“平底型”函数.
为“平底型”函数.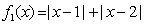 ,
,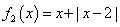 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;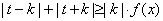 ,(
,(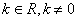 )
)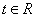 恒成立,求实数
恒成立,求实数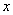 的范围;
的范围;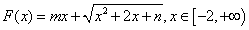 是“平底型”函数,求
是“平底型”函数,求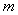 和
和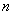 的值.
的值.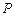 与日产量
与日产量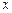 的函数关系是
的函数关系是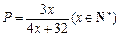 .
. 的球的内接圆柱,问圆柱的底半径与高多大,才能使圆柱的体积最大。
的球的内接圆柱,问圆柱的底半径与高多大,才能使圆柱的体积最大。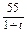 (单位:m/s)紧急刹车至停止.求:
(单位:m/s)紧急刹车至停止.求: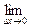
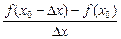 的值是
的值是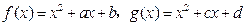 ,且
,且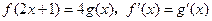 ,
,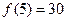 .
.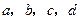 的值.
的值.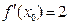 ,则
,则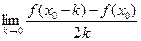 等于( )
等于( )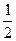
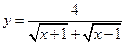 的导数.
的导数.