题目内容
已知
(1)证明: ⊥
⊥ ;
;
(2)若存在实数k和t,满足
 且
且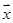 ⊥
⊥ ,试求出k关于t的关系式k=f(t).
,试求出k关于t的关系式k=f(t).
(3)根据(2)的结论,试求出k=f(t)在(-2,2)上的最小值.

(1)证明:
 ⊥
⊥ ;
;(2)若存在实数k和t,满足

 且
且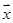 ⊥
⊥ ,试求出k关于t的关系式k=f(t).
,试求出k关于t的关系式k=f(t).(3)根据(2)的结论,试求出k=f(t)在(-2,2)上的最小值.
(1)详见解析,(2) (3)
(3) .
.
 (3)
(3) .
.试题分析:(1)利用向量数量积得:
 因为
因为 ,所以
,所以 (2)由
(2)由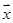 ⊥
⊥ 可列k关于t的关系式k=f(t).本题若注意到
可列k关于t的关系式k=f(t).本题若注意到 则不需将
则不需将 的坐标代入,而是将
的坐标代入,而是将 整体化简,即
整体化简,即 (3)首先将函数变量分离,即
(3)首先将函数变量分离,即 ,再利用对勾函数的单调性得出函数的最小值.利用函数单调性定义证明其增减性,先分区间
,再利用对勾函数的单调性得出函数的最小值.利用函数单调性定义证明其增减性,先分区间 和
和 ,再设区间
,再设区间 上任意两个数
上任意两个数 ,作差变形后判断符号.即
,作差变形后判断符号.即 ,由于
,由于 所以
所以 ,因此
,因此 ,也就是函数在
,也就是函数在 单调递增,同理可得函数在
单调递增,同理可得函数在 单调递减.
单调递减.试题解析:(1)


(2)

(3)



练习册系列答案
相关题目
 ,求
,求 的值。
的值。 ,B
,B ,C
,C ,则△ABC的形状是( )
,则△ABC的形状是( ) ,1),b是不平行于x轴的单位向量,且a·b=
,1),b是不平行于x轴的单位向量,且a·b=


 ,
, ,M、N分别是BC边上的三等分点,则
,M、N分别是BC边上的三等分点,则 的值是( )
的值是( )
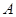 、
、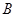 、
、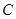 为直线
为直线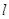 上不同的三点,点
上不同的三点,点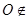 直线
直线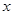 满足关系式
满足关系式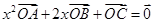 ,有下列命题:
,有下列命题: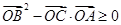 ; ②
; ② 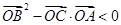 ;
;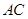 的中点.
的中点. ,(a+b)⊥(2a-b),则向量a与b的夹角为()
,(a+b)⊥(2a-b),则向量a与b的夹角为() ,则角A的最大值为( )
,则角A的最大值为( ) 



 满足
满足 且
且 ,则
,则 ( )
( )