题目内容
有以下说法:
①函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,则a≤1.
②若f(x)是定义在R上的奇函数,若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,则a+b=0.
③函数f(x)在(0,+∞)上的单调增函数,若x1,x2∈(0,+∞),且f(x1)<f(x2),则x1<x2.
④函数f(x)=
在(3,+∞)上为增函数.
其中正确的是______(只填代号)
①函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,则a≤1.
②若f(x)是定义在R上的奇函数,若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,则a+b=0.
③函数f(x)在(0,+∞)上的单调增函数,若x1,x2∈(0,+∞),且f(x1)<f(x2),则x1<x2.
④函数f(x)=
| x+2 |
| x+3 |
其中正确的是______(只填代号)
①∵函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,
∴
≤1,解得a≤2.故①不成立;
②若f(x)是定义在R上的奇函数,
若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,
则a与b互为相反数,所以a+b=0.故②正确;
③∵函数f(x)在(0,+∞)上的单调增函数,
x1,x2∈(0,+∞),且f(x1)<f(x2),
∴由增函数的性质知x1<x2.故③正确;
④∵函数f(x)=
=1-
,
∴函数f(x)=
在(3,+∞)上为增函数,故④正确.
故答案为:②③④.
∴
| a |
| 2 |
②若f(x)是定义在R上的奇函数,
若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,
则a与b互为相反数,所以a+b=0.故②正确;
③∵函数f(x)在(0,+∞)上的单调增函数,
x1,x2∈(0,+∞),且f(x1)<f(x2),
∴由增函数的性质知x1<x2.故③正确;
④∵函数f(x)=
| x+2 |
| x+3 |
| 1 |
| x+3 |
∴函数f(x)=
| x+2 |
| x+3 |
故答案为:②③④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
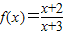 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.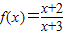 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.