题目内容
有以下说法:①函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,则a≤1.
②若f(x)是定义在R上的奇函数,若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,则a+b=0.
③函数f(x)在(0,+∞)上的单调增函数,若x1,x2∈(0,+∞),且f(x1)<f(x2),则x1<x2.
④函数
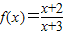 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.其中正确的是 (只填代号)
【答案】分析:①由函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,知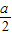 ≤1,由此能判断①的正误;
≤1,由此能判断①的正误;
②f(x)是定义在R上的奇函数,利用奇函数的性质判断②的正误;
③函数f(x)在(0,+∞)上的单调增函数,利用增函数的性质判断③的正误;
④由函数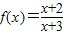 =1-
=1-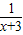 ,知函数
,知函数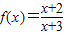 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.
解答:解:①∵函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,
∴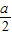 ≤1,解得a≤2.故①不成立;
≤1,解得a≤2.故①不成立;
②若f(x)是定义在R上的奇函数,
若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,
则a与b互为相反数,所以a+b=0.故②正确;
③∵函数f(x)在(0,+∞)上的单调增函数,
x1,x2∈(0,+∞),且f(x1)<f(x2),
∴由增函数的性质知x1<x2.故③正确;
④∵函数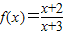 =1-
=1-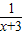 ,
,
∴函数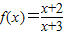 在(3,+∞)上为增函数,故④正确.
在(3,+∞)上为增函数,故④正确.
故答案为:②③④.
点评:本题考查命题的真假的判断,解题时要认真审题,注意函数的单调性、奇偶性的合理运用.
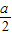 ≤1,由此能判断①的正误;
≤1,由此能判断①的正误;②f(x)是定义在R上的奇函数,利用奇函数的性质判断②的正误;
③函数f(x)在(0,+∞)上的单调增函数,利用增函数的性质判断③的正误;
④由函数
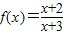 =1-
=1-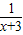 ,知函数
,知函数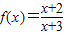 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.解答:解:①∵函数f(x)=x2-ax+1在区间[1,+∞)上为增函数,
∴
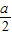 ≤1,解得a≤2.故①不成立;
≤1,解得a≤2.故①不成立;②若f(x)是定义在R上的奇函数,
若在(0,+∞)上有最小值a,在(-∞,0)上有最大值b,
则a与b互为相反数,所以a+b=0.故②正确;
③∵函数f(x)在(0,+∞)上的单调增函数,
x1,x2∈(0,+∞),且f(x1)<f(x2),
∴由增函数的性质知x1<x2.故③正确;
④∵函数
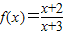 =1-
=1-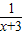 ,
,∴函数
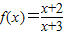 在(3,+∞)上为增函数,故④正确.
在(3,+∞)上为增函数,故④正确.故答案为:②③④.
点评:本题考查命题的真假的判断,解题时要认真审题,注意函数的单调性、奇偶性的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
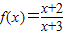 在(3,+∞)上为增函数.
在(3,+∞)上为增函数.