题目内容
【题目】已知直线l过点A(2,4),且被平行直线l1:x-y+1=0与l2:x-y-1=0所截的线段中点M在直线x+y-3=0上,求直线l的方程.
【答案】解:解法一:∵点M在直线x+y-3=0上,∴设点M坐标为(t,3-t),由题意知点M到l1 , l2的距离相等,即 ![]() ,解得t=
,解得t= ![]() ,∴
,∴ ![]() .又l过点A(2,4),由两点式得
.又l过点A(2,4),由两点式得 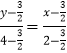 ,
,
即5x-y-6=0,故直线l的方程为5x-y-6=0.
解法二:设与l1 , l2平行且距离相等的直线为l3:x-y+C=0,由两平行直线间的距离公式得 ![]() ,解得C=0,即l3:x-y=0.
,解得C=0,即l3:x-y=0.
由题意得中点M在l3上,又点M在x+y-3=0上.
解方程组 ![]() 得
得 ![]() ∴
∴ ![]() .
.
又l过点A(2,4),故由两点式得直线l的方程为5x-y-6=0
【解析】设出点M的坐标为(t,3-t),结合条件得到关于t的方程,求出t的值,再由两点式得到直线方程.
【考点精析】解答此题的关键在于理解两点式方程的相关知识,掌握直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2,以及对点到直线的距离公式的理解,了解点
则:y-y1/y-y2=x-x1/x-x2,以及对点到直线的距离公式的理解,了解点![]() 到直线
到直线![]() 的距离为:
的距离为: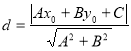 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目