题目内容
(本小题满分13分)已知函数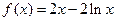

(Ⅰ)求函数在点(1,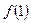 )处的切线方程
)处的切线方程
(Ⅱ)求函数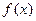 的极值
的极值
(Ⅲ)对于曲线上的不同两点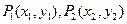 ,如果存在曲线上的点
,如果存在曲线上的点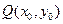 ,且
,且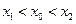 ,使得曲线在点
,使得曲线在点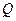 处的切线
处的切线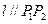 ,则称
,则称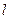 为弦
为弦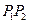 的陪伴切线.已知两点
的陪伴切线.已知两点
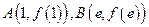 ,试求弦
,试求弦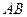 的陪伴切线
的陪伴切线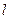 的方程;
的方程;
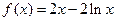

(Ⅰ)求函数在点(1,
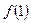 )处的切线方程
)处的切线方程(Ⅱ)求函数
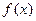 的极值
的极值(Ⅲ)对于曲线上的不同两点
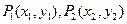 ,如果存在曲线上的点
,如果存在曲线上的点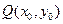 ,且
,且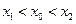 ,使得曲线在点
,使得曲线在点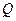 处的切线
处的切线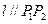 ,则称
,则称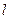 为弦
为弦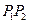 的陪伴切线.已知两点
的陪伴切线.已知两点
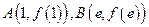 ,试求弦
,试求弦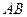 的陪伴切线
的陪伴切线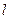 的方程;
的方程;解:(I)y=2…………………………………(4分)
(Ⅱ) . ……………………………(6分)
. ……………………………(6分)
 得
得 .
.
当 变化时,
变化时, 与
与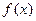 变化情况如下表:
变化情况如下表:

当x=1时,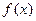 取得极小值
取得极小值 . 没有极大值. ……………………(9分)
. 没有极大值. ……………………(9分)
(Ⅲ)设切点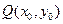 ,则切线
,则切线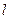 的斜率为
的斜率为 .
.
弦AB的斜率为 . …(10分)
. …(10分)
由已知得, ,则
,则 =
= ,解得
,解得 ,…………(12分)
,…………(12分)
所以,弦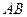 的伴随切线
的伴随切线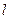 的方程为:
的方程为: .……(13分)
.……(13分)
(Ⅱ)
 . ……………………………(6分)
. ……………………………(6分) 得
得 .
.当
 变化时,
变化时, 与
与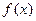 变化情况如下表:
变化情况如下表:
当x=1时,
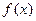 取得极小值
取得极小值 . 没有极大值. ……………………(9分)
. 没有极大值. ……………………(9分)(Ⅲ)设切点
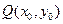 ,则切线
,则切线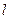 的斜率为
的斜率为 .
.弦AB的斜率为
 . …(10分)
. …(10分)由已知得,
 ,则
,则 =
= ,解得
,解得 ,…………(12分)
,…………(12分)所以,弦
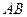 的伴随切线
的伴随切线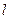 的方程为:
的方程为: .……(13分)
.……(13分)略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 的部分图象,则函数
的部分图象,则函数 的零点所
的零点所




 则
则 的大小关系是( )
的大小关系是( )



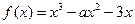
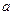 =2时,求
=2时,求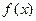 的零点;
的零点;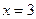 是
是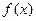 的极值点,求
的极值点,求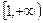 上是增函数,求实数
上是增函数,求实数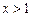 ,则
,则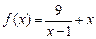 的最小值为 。
的最小值为 。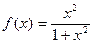 ,那么
,那么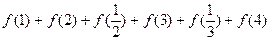
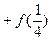 =______________
=______________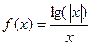 的图象可能是
的图象可能是 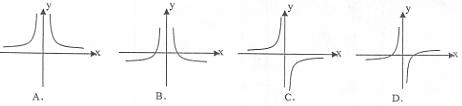
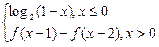 ,则f(2012)的值为( )
,则f(2012)的值为( )