题目内容
函数 与
与 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
A. | B. |
C. | D. |
A
解析试题分析:根据函数 与
与 在区间[1,2]上都是减函数,那么可知[1,2]是二次函数减区间的一个子区间,而其开口向下,对称轴为x=a,那么可知
在区间[1,2]上都是减函数,那么可知[1,2]是二次函数减区间的一个子区间,而其开口向下,对称轴为x=a,那么可知 ,而对于
,而对于 在给定区间是递减,则说明了2a+1>0,a>-
在给定区间是递减,则说明了2a+1>0,a>- ,综上可知,那么参数a的范围是
,综上可知,那么参数a的范围是 ,选A.
,选A.
考点:二次函数
点评:主要是考查了开口向下的二次函数在对称轴右边为减函数,在对称轴左边为增函数.

练习册系列答案
相关题目
下列各组函数是同一函数的是
① 与
与 ;②
;② 与
与 ;③
;③ 与
与 ;④
;④ 与
与 。
。
| A.①② | B.①③ | C.②③④ | D.①④ |
下列函数中,在其定义域内既是奇函数又是减函数的是
A. | B. | C. | D. |
函数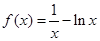 的零点个数为( )
的零点个数为( )
A. | B. | C.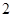 | D.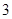 |
下列函数中,在区间 上为增函数的是( ).
上为增函数的是( ).
A.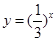 | B.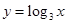 | C.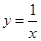 | D.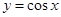 |
函数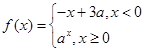
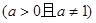 是R上的减函数,则a的取值范围是( )
是R上的减函数,则a的取值范围是( )
| A.(0,1) | B.[ 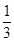 ,1) ,1) | C.(0,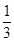 ] ] | D.( 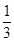 ,1) ,1) |
函数满足f(x)f(x+2)=13,若f(3)=2,则f(2013)= ( )
| A.13 | B.2 | C. | D. |
已知y=f(x)是奇函数,当x>0时,f(x)=2x(1-x),当x<0时f(x)应该等于 ( )
| A.–2x(1-x) | B.2x(1-x) | C.–2x(1+x) | D.2x(1+x) |
 的定义域为 ( )
的定义域为 ( )