题目内容
如图，已知E是△ABC的内心，∠A的平分线交BC于点F，且与△ABC的外接圆相交于点D.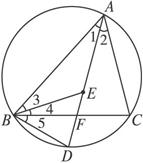
（1）求证：∠DBE＝∠DEB；
（2）若AD＝8 cm，DF∶FA＝1∶3.求DE的长.
思路解析：由内心、圆周角转化为若干角相等，易证△BED∽△ABD.
（1）证明：∵E是△ABC的内心，
∴∠1=∠2,∠3=∠4.
∵∠BED=∠3+∠1,∠5=∠2，
∴∠4+∠5=∠3+∠2=∠3+∠1，
即∠EBD=∠BED.
（2）解：∵∠EBD=∠BED，∴DE=DB.
∵∠D=∠D,∠5=∠2=∠1，
∴△BED∽△ABD.
∴BD2=AD·FD.
∵DF∶FA=1∶3，AD=8，
∴DF∶AD=1∶4.
∴
，解得DF=2(cm).
∴BD2=8×2=16，DE=BD=4(cm).
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
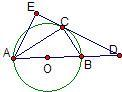如图，已知⊙O是△ABC的外接圆，AB是⊙O的直径，D是AB延长线上一点，AE⊥DC交DC的延长线于点E，且AC平分∠EAB．
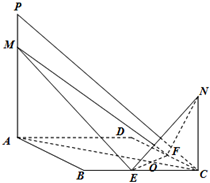如图，已知E，F分别是正方形ABCD边BC、CD的中点，EF与AC交于点O，PA、NC都垂直于平面ABCD，且PA=AB=4，NC=2，M是线段PA上一动点．
如图，已知ABCD是边长为a的正方形，E，F分别是AB，AD的中点，CG⊥面ABCD，CG=a．
（2013•许昌三模）如图，已知C是以AB为直径的半圆O上一点，CH⊥AB于点H，直线AC与过B点的切线相交于点D，E为CH中点，连接AE并延长交BD于点F，直线CF交直线AB于点G．