Question

如图，已知ABCD是边长为a的正方形，E，F分别是AB，AD的中点，CG⊥面ABCD，CG=a．
（1）求证：BD∥EFG；
（2）求点B到面GEF的距离．

Answer 1

分析：（1）要证BD∥平面EFG，只需证明平面EFG外的直线BD平行平面EFG那地方直线EF 即可；
（2）求点B到面GEF的距离，就是求C到平面EFG距离的

1

3

，直接作垂线求解即可．

解答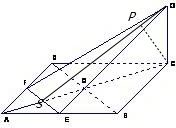：证明（1）∵E，F分别是AB，AD的中点，∴EF∥BD，
∵EF?平面EFG，BD不在平面EFG，∴BD∥平面EFG；
（2）E，F分别是AB，AD的中点，O到面GEF的距离，
就是B面GEF的距离，也就是C面GEF的距离的

1

3

AS=

2 a

2

，GS=

a2+( 3 2 a 4 )2

=

34 a

4

作CP⊥GS于P，则CP就是C面GEF的距离，
GS•CP=CG•SC
即：

34 a

4

PC=a•

3 2 a

4

PC=

3 17 a

17

所以点B到面GEF的距离：

17 a

17

点评：本题考查直线与平面垂直，点到平面的距离，考查空间想象能力，是中档题．